#15 虚根の数え上げ、そして代数閉体へ(前編)
これまでは代数的実数について扱ってきたが、(複素数の範囲での)代数的数も考えよう。 #0 に書いたように、代数的数 \overline{\mathbf{Q}} も計算機で正確に取り扱える。
代数的数の表し方と四則演算
計算機で複素数を扱う場合は、実部と虚部の組で表すのが普通だろう。 代数的数の場合も、 i. 代数的実数を2つ使って実部と虚部を表す、という手がある。 あるいは、実数の場合に「多項式と、分離区間」としていたのを拡張し、 ii. 「多項式と、根を分離する(複素平面上の)長方形」の組として表す、という手もある。
- 実部の最小多項式、実部の分離区間、虚部の最小多項式、虚部の分離区間
- 最小多項式、分離領域(長方形など)

もちろん、どちらの方法でも同じ代数的数を表すことができ、相互変換も可能である:
定理. 代数的数 \alpha の実部 \operatorname{Re}\alpha と虚部 \operatorname{Im}\alpha はそれぞれ代数的実数である。 また、代数的実数 x, y に対して、 x+\sqrt{-1}y は代数的数である。
証明. 前半について、 \alpha の定義多項式を f(x)=a_nx^n+\cdots+a_1x+a_0\in\mathbf{Z}[x] とすると、複素共役 \overline{\alpha} も同じ多項式 f の根である。 特に、 \overline{\alpha} は代数的数である。
また、虚数単位 \sqrt{-1} は多項式 x^2+1 の根であるので代数的数である。
#3 で代数的数同士の加減乗除はまた代数的数であることを示したので、 \operatorname{Re}\alpha=\frac{\alpha+\overline{\alpha}}{2} と \operatorname{Im}\alpha=\frac{\alpha-\overline{\alpha}}{2\sqrt{-1}} も代数的数である。 これらはもちろん実数なので、代数的実数である。
後半は明らかである。
実部と虚部、複素共役
代数的数 \alpha の実部 \operatorname{Re}\alpha, 虚部 \operatorname{Im}\alpha, 複素共役 \overline{\alpha} をどのように表せるか考えよう。 \alpha の最小多項式を f(x)=a(x-\alpha_1)\cdots(x-\alpha_n)\in\mathbf{Z}[x] とする。
まず、複素共役 \overline{\alpha} の最小多項式は f 自身である。 f の係数が実数であるから \overline{\alpha} は f の根となるし、 f は \mathbf{Z} 上既約なのでそれが最小多項式である。 f の根は実軸に関して対称に存在するので、分離領域については、単純に虚部の符号を反転させれば良い。
実部 \operatorname{Re}\alpha=\frac{\alpha+\overline{\alpha}}{2} は \begin{aligned} F(x)&=2^{n^2}a^{n}\prod_{i,j}\left(x-\frac{\alpha_i+\alpha_j}{2}\right) \\ &=\operatorname{res}_y\Bigl(f(y),2^n\prod_j\left(x-\frac{y+\alpha_j}{2}\right)\Bigr) \\ &=\operatorname{res}_y\Bigl(f(y),\prod_j(2x-y-\alpha_j)\Bigr) \\ &=\operatorname{res}_y(f(y),f(2x-y)) \end{aligned} の実根となる。
f の根 \alpha_i は全て F の根でもある。 従って、F は f で割り切れる。 i\ne j の場合、 \frac{\alpha_i+\alpha_j}{2} は F の重根である。 従って F/f は平方、つまりある多項式 g について F/f=g^2 と書ける。
虚部 \operatorname{Im}\alpha=\frac{\alpha-\overline{\alpha}}{2\sqrt{-1}} は \begin{aligned} G(x)&=(-2\sqrt{-1})^{n^2}a^{n}\prod_{i,j}\left(x-\frac{\alpha_i-\alpha_j}{2\sqrt{-1}}\right) \\ &=\operatorname{res}_y\Bigl(f(y),(-2\sqrt{-1})^n a\prod_j\left(x-\frac{y-\alpha_j}{2\sqrt{-1}}\right)\Bigr) \\ &=\operatorname{res}_y\Bigl(f(y),a\prod_j(-2\sqrt{-1}x+y-\alpha_j)\Bigr) \\ &=\operatorname{res}_y(f(y),f(y-2\sqrt{-1}x)) \end{aligned} の実根となる。
多項式 \operatorname{res}_y(f(y),f(y-2\sqrt{-1}x)) の係数は複素数となる。 複素数係数多項式の実根というのは、実部 \operatorname{Re}G と虚部 \operatorname{Im}G に共通する根である。 計算には、 \gcd(\operatorname{Re}G, \operatorname{Im}G) の根を計算すれば良い。
G の定義で積を取っているが、 i=j の場合は \frac{\alpha_i-\alpha_j}{2\sqrt{-1}}=0 である。 そのため、G(x) は x^n で割り切れる。 i\ne j の場合を考えると、 G(x)/x^n は \left(x-\frac{\alpha_i-\alpha_j}{2\sqrt{-1}}\right)\left(x-\frac{\alpha_j-\alpha_i}{2\sqrt{-1}}\right) =x^2-\left(\frac{\alpha_i-\alpha_j}{2\sqrt{-1}}\right)^2 =x^2+\left(\frac{\alpha_i-\alpha_j}{2}\right)^2 の積で書ける。 よって、 G(x)/x^n は x^2 についての多項式として書けるはずである。
代数的数の演算
代数的数に関する基本的な演算(四則演算)について考えよう。
代数的数を代数的実数の組(実部、虚部)で表す場合は、すでに実装した代数的実数の四則演算を利用して、 \begin{aligned} (x+\sqrt{-1}y)\pm(x'+\sqrt{-1}y')&=(x\pm x')+\sqrt{-1}(y\pm y'), \\ (x+\sqrt{-1}y)(x'+\sqrt{-1}y')&=(xx'-yy')+\sqrt{-1}(xy'+yx'), \\ \frac{1}{x+\sqrt{-1}y}&=\frac{x-\sqrt{-1}y}{x^2+y^2} \end{aligned} とすれば良い。
代数的数を最小多項式1個と分離領域で表す場合、 #3, #6 で見たのと同じように、終結式を使って最小多項式を計算する方法を使える。 分離領域に関しては、区間演算および計算可能実数の複素数バージョンを実装すれば良い。 (こちらは、単に実部と虚部を区間・計算可能実数で表すので良いだろう)
代数的数を係数とする多項式の根
代数的数の四則演算はすでに述べた方法で実装できる。 代数的数が代数閉体 (algebraically closed field) であるためには、あとは「代数的数を係数とする多項式の根を求める」操作が必要である。
この問題は、前回のように終結式を繰り返し使えば、多項式の係数から代数的数を消去し、「整数係数多項式の根を求める」問題に帰着できる。
与えられた(整数または代数的実数係数の)多項式の「実」根を列挙するアルゴリズムは、 #2 と #14 でそれぞれ取り上げたが、今回は複素数の範囲での根を全て求めたい。 そのための考えられる方針は2つある:
方針1:f(x+\sqrt{-1}y)=0 を、 x,y についての実2変数連立方程式とみなして解く。
方針2:複素数の領域についてのスツルムの定理の一般化を考え、複素数の範囲で根を絞り込む。
順番に見ていこう。
方針1:実2変数連立方程式
実2変数の実数値関数 u, v を \begin{aligned} u(x,y)&:=\operatorname{Re}f(x+\sqrt{-1}y), \\ v(x,y)&:=\operatorname{Im}f(x+\sqrt{-1}y) \end{aligned} と置く。f が多項式なので、 u, v は2変数の多項式である。
解きたい方程式は \begin{aligned} u(x,y)&=0, \\ v(x,y)&=0 \end{aligned} であるが、我々がこれまで実装してきたのは「1変数の方程式を解く」操作である。 そこで、この連立方程式を1変数の方程式に帰着させよう。
y を固定した時の u(x,y)=0 の根を(重複を込めて) x=\alpha_1,\ldots,\alpha_n とする。 すると、 v にこの根を代入したものの積 v(\alpha_1,y)v(\alpha_2,y)\cdots v(\alpha_n,y)=\prod_{i=1}^n v(\alpha_i,y) は、終結式により \operatorname{res}_x(u(x,y),v(x,y)) と書ける。 これは y についての一変数多項式なので、これまでの方法で実根を計算できる。
そうして計算した根 y=\beta_1,\ldots,\beta_m のそれぞれを u に代入すれば、 x についての一変数多項式が得られるので、それを解けば良い。
方針1はこれまでの知識を少し応用すればできるが、代数的数の大事な性質を失っているように思えてならない。 そのため、今後はもっぱら、方針2を考えていく。
方針2:虚根の数え上げ
実根の分離区間というものは、2個の実数(有理数)を指定すれば決まってしまう。 しかし、複素数の範囲になると、根を分離するのは領域(連結開集合)であり、様々な形状がありうる。
問題としては、単純(つまり、自分自身と交わらない)閉曲線 C を考え、それが内側に見る領域に含まれる根の個数を決定したい。

そのためにまず、「一般 Sturm 列」と「回転数」の概念を準備しておく。
一般 Sturm 列
#2 で見た Strum 列は、多項式 f とその微分 f' から始まった。 その定義を変え、はじめの2つ f_0, f_1 がより一般の実係数多項式であるような列を考えよう。
- f_0 と f_1 は共通の実根を持たない
- 1\le i について f_{i-1}=q_i f_i-f_{i+1},\ \deg f_{i+1}<\deg f_i (つまり、 f_{i+1} は f_{i-1} の f_i による剰余の符号を逆転させたもの)
- f_{l+1}=0
この時、以下が成り立つ:
- f_i と f_{i+1} は共通の実根を持たない。特に、 f_l は符号が一定である。
- 実数 a について f_i(a)=0 であれば、 f_{i-1}(a)f_{i+1}(a)<0 である。
(例によって f_i の正の実数倍は関係ないので、符号さえどうにかすれば、好きな多項式剰余列で考えて良い)
この多項式列 \{f_0,f_1,\ldots,f_l\} を一般 Sturm 列と呼ぶことにする。 (一般化されたものも単に「Sturm 列」と呼んでもいいかもしれない)
f_0 の実根 \alpha について、整数 \chi(f_0,f_1;\alpha) を
- f_0(x)/f_1(x) の符号が x=\alpha の前後で変わらないならば、 \chi(f_0,f_1;\alpha)=0
- f_0(x)/f_1(x) の符号が x=\alpha の前後で - から + に変わるならば、 \chi(f_0,f_1;\alpha)=+1
- f_0(x)/f_1(x) の符号が x=\alpha の前後で + から - に変わるならば、 \chi(f_0,f_1;\alpha)=-1
と定義する。 f_0,f_1 が文脈から明らかならば、 f_0,f_1 を省略して単に \chi(\alpha) と書くことにする。
幾何学的な説明を試みるなら、平面上で、 x で径数づけされた曲線 (f_0(x),f_1(x)) を考えるのが適当だろう。 曲線が第1象限と第2象限、第3象限と第4象限を行き来する際、整数 \chi の割り当て方は次のようになる:

図の中の V は、それぞれの象限における実数列 \{f_0(x),f_1(x)\} の符号の変化の数を表す。
準備が済んだところで、 Sturm の定理の一般化をしよう。 Sturm の定理は実根の個数を数えるものだったが、その一般化は整数 \chi の総和を数える。定理. 多項式 f_0,f_1\in\mathbf{R}[x] は互いに素であるとし、 f_0,f_1 から始まる一般 Sturm 列を \{f_0,f_1,\ldots,f_l\} とする。 実数 t について自然数 V(f_0,f_1;t) を、実数列 \{f_0(t),f_1(t),\ldots,f_l(t)\} の符号の変化の数と定める。 f_0 の根でない実数 a,b\ (a<b) について、 V(f_0,f_1;a)-V(f_0,f_1;b) は区間 (a,b) における \chi(f_0,f_1;\alpha) の総和を与える: V(f_0,f_1;a)-V(f_0,f_1;b)=\sum_{\begin{array}{c}\scriptstyle\alpha\in(a,b),\\\scriptstyle\alpha\text{ is a root of }f_0\end{array}} \chi(f_0,f_1;\alpha). %V(b)-V(c)=\sum_{\substack{\alpha\in(a,b),\\\alpha\text{ is a root of }f_0}} \chi(\alpha).
証明. V が変化しうるのは、ある i について f_i(a)=0 となるような a においてである。 そこで、 f_i(a)=0 となるような任意の i と a\in\mathbf{R} について、
- i=0 ならば a の前後で V が減少する(\{f_0(t),f_1(t)\} の符号の変化の数が t<a と a\le t で異なる)
- i>0 ならば、 f_i に起因する V の変化は起こらない(同じ a に関して f_0(a)=0 となって V が変化する可能性は否定しない)
ことを示す。
i=0 の場合。 f_0/f_1 の a の近傍における符号を表にしてみよう。 ただし、 \varepsilon は十分小さい正の数とするし、表の中の V は部分列 \{f_0,f_1\} の符号の変化の数である。 また、それぞれの表において、複号同順とする。
\chi(a)=+1 の場合:
| t | a-\varepsilon | a | a+\varepsilon |
|---|---|---|---|
| f_0 | ∓ | 0 | ± |
| f_1 | ± | ± | ± |
| f_0/f_1 | − | 0 | + |
| V | 1 | 0 | 0 |
\chi(a)=-1 の場合:
| t | a-\varepsilon | a | a+\varepsilon |
|---|---|---|---|
| f_0 | ± | 0 | ∓ |
| f_1 | ± | ± | ± |
| f_0/f_1 | + | 0 | − |
| V | 0 | 0 | 1 |
\chi(a)=0 の場合A:
| t | a-\varepsilon | a | a+\varepsilon |
|---|---|---|---|
| f_0 | ± | 0 | ± |
| f_1 | ± | ± | ± |
| f_0/f_1 | + | 0 | + |
| V | 0 | 0 | 0 |
\chi(a)=0 の場合B:
| t | a-\varepsilon | a | a+\varepsilon |
|---|---|---|---|
| f_0 | ± | 0 | ± |
| f_1 | ∓ | ∓ | ∓ |
| f_0/f_1 | − | 0 | − |
| V | 1 | 0 | 1 |
いずれの場合も、部分列 \{f_0(t),f_1(t)\} の t=a-\varepsilon から t=a+\varepsilon にかけての符号の変化の数は、 \chi(a) だけ減少していることが表からわかる。
i>0 の場合。 f_i と f_{i-1} は互いに素なので、 f_{i-1}(a)\ne 0 である。 a の前後で f_{i-1} と f_{i+1} の符号は変化しないこと、そして f_{i-1}(a) と f_{i+1}(a) の符号は逆であることに注意する。
これらを踏まえて、f_{i-1}, f_i 及び f_{i+1} の a の近傍における符号を表にしてみよう。 ただし、 ? には、それぞれ任意の符号が入る。
| t | a-\varepsilon | a | a+\varepsilon |
|---|---|---|---|
| f_{i-1} | ± | ± | ± |
| f_i | ? | 0 | ? |
| f_{i+1} | ∓ | ∓ | ∓ |
| V | 1 | 1 | 1 |
いずれの場合も、部分列 \{f_{i-1}(t),f_i(t),f_{i+1}(t)\} の符号の変化の数は t=a の近傍で 1 のまま変化しない。
#2 で見た Sturm の定理は、 f_1=f_0' という特殊な場合であった。 #2 の f_1=f_0' の場合と、今回の一般化された場合を比較すると、
- f_1=f_0' の場合は \chi(\alpha)=1 の場合しかありえなかったが、一般化すると \chi(\alpha)=0,-1 の場合が出てくる
- f_1=f_0' の場合は f_0 と f_1 が互いに素という条件から f_0 が重根を持たないことが言えたが、一般化するとそうではなくなる
- f_1=f_0' の場合は端点に f_0 の根がある場合でも定理の主張を半開区間 (b,c] に拡張できたが、一般化すると一筋縄では行かなくなる
となる。
#2 での Sturm の定理を今回の一般化された枠組みで捉えるために、多項式とその微分から始まる Sturm 列がどうなるか見てみよう。 多項式 f(x)=3x^{5}-45x^{4}+214x^{3}-282x^{2}-217x^{1}+327 について (f(x),f'(x)) をプロットすると次のようになる:

多項式とその微分 f,f' から始まる Sturm 列について、整数 \chi は常に +1 となることが見て取れる。 従って、その和は f の実根を単純に数えたもの(= 3 個)と一致する。
余談:Cauchy 指数
関連する概念として、 Cauchy 指数というものがあるようなので、一応触れておく。
(TODO: 「とある有理関数のコーシー指数」のロゴを作る)
実係数有理関数 f と実数の区間 (a,b) について、区間の端点は f の極ではないとする。 この時、区間 (a,b) における Cauchy 指数 (Cauchy index) I_a^b f を、区間内の極における \iota の総和と定める: I_a^b f:=\sum_{\begin{array}{c}\scriptstyle\alpha\in(a,b),\\\scriptstyle\alpha\text{ is a pole of }f\end{array}} \iota(\alpha). %I_a^b f:=\sum_{\substack{\alpha\in(a,b),\\\alpha\text{ is a pole of }f_0}} \iota(\alpha).
ただし、 f の極 \alpha について、整数 \iota(\alpha) は次のように定める:
- f が \alpha において -\infty から +\infty に跳ぶ、つまり \lim_{x\to \alpha-0} f(x)=-\infty, \quad \lim_{x\to \alpha+0} f(x)=+\infty となる場合、 \iota(\alpha)=+1.
- f が点 \alpha において +\infty から -\infty に跳ぶ、つまり \lim_{x\to \alpha-0} f(x)=+\infty, \quad \lim_{x\to \alpha+0} f(x)=-\infty となる場合、 \iota(\alpha)=-1.
- それ以外の場合は \iota(\alpha)=0.
Cauchy 指数は、一般 Sturm 列により計算できる。 有理関数 f を互いに素な多項式 g, h を使って f=\frac{h}{g} と表したとする。 f の極はすなわち g の根であるから、先ほどの記号を使えば \iota(\alpha)=\chi(g,h;\alpha) である。 よって、 Cauchy 指数は、一般 Sturm 列の符号の変化の数 V(g,h;t) を使い、 I_a^b f=V(g,h;a)-V(g,h;b) と計算できる。
なお、 a や b が \pm\infty の時も Cauchy 指数を定義できる。
回転数
a を複素平面の点とし、閉曲線 C は a を通らないとする。 この時、曲線 C は a の周りを「何周か」している。 この「何周か」という整数を、 a に関する C の回転数(winding number; 直訳は「巻き数」だろうか)と呼び、 n(C,a) で表す。 曲線の向きに関しては、正の向き(反時計回り)の巻きつきを正の整数で表し、負の向き(時計回り)の巻きつきを負の整数で表す。
例えば、曲線1は原点の周りを「2周」しているというのは直観的に明らかだろう。 したがって曲線1の原点に関する回転数は 2 である。

曲線2は少々複雑だが、進んで戻った分を相殺すれば、結局は原点の周りを「1周」しかしていない。 したがって曲線2の原点に関する回転数は 1 である。

一方、曲線3は原点の周りを巻きついていない。 これは「0周」していると呼ぶべきだろう。 つまり、曲線3の原点に関する回転数は 0 である。

「何周か」という定義はあまりにもふわふわしているので、より厳密な定義を考えよう。 曲線上の点を点 a から見た時の角度(偏角) \arg(C(t)-a) を符号を込めて考え、偏角の変化 \Delta\arg(C(t)-a) の総和を考える。 曲線が閉じていることから、この値は 2\pi の整数倍となるはずで、その「何倍か」の整数が先の「何周か」に対応していると考えられる。

残念ながら偏角 \arg を(原点を除いた)複素平面全体でうまく定義することはできず、普通はどこか(典型的には、負の実軸)に切れ込みを入れた分枝を考える。 すると、その部分で \arg(C(t)-a) の値がジャンプしてしまい、 \Delta\arg(C(t)-a) の和は結局 0 となる。 これでは、回転数は得られない。
この辺の詳細は複素解析の教科書を参照してほしいが、ざっくり言うと、 \frac{1}{z-a} の積分 \int_C\frac{dz}{z-a} は 2\pi\sqrt{-1} の整数倍となる。 そして、それを利用して回転数を定義する: n(C,a):=\frac{1}{2\pi\sqrt{-1}}\int_C\frac{dz}{z-a}.
回転数と複素関数の零点
回転数と多項式の根の関係を見ていこう、と言いたいところだが、せっかくなので「多項式の根」を「複素関数の零点」に一般化して考える。
単純閉曲線 C の上と内部で正則な関数 f を考える。 ただし、 C の上では f は零点を持たないとする。 C の内部には重複を込めて n 個の零点 \alpha_1,\ldots,\alpha_n があるとして、 f を f(z)=(z-\alpha_1)\cdots(z-\alpha_n)g(z) と書く。 ただし、 g は C の上と内部で 0 にならない正則関数である。 このとき、fの対数微分を C に沿って積分したもの \int_C \frac{f'(z)}{f(z)}dz を考えよう。
まず、 f の微分は f'(z)=\sum_{i=1}^n (z-\alpha_1)\cdots(z-\alpha_{i-1})(z-\alpha_{i+1})\cdots(z-\alpha_n)g(z)+(z-\alpha_1)\cdots(z-\alpha_n)g'(z) なので、 \frac{f'(z)}{f(z)}=\sum_{i=1}^n \frac{1}{z-\alpha_i}+\frac{g'(z)}{g(z)} である。 これを積分すれば、回転数の定義より \begin{aligned} \int_C \frac{f'(z)}{f(z)}dz &=\sum_{i=1}^n \int_C \frac{dz}{z-\alpha_i}+\int_C \frac{g'(z)}{g(z)}dz \\ &=2\pi\sqrt{-1}\sum_{i=1}^n n(C,\alpha_i) \end{aligned} となる。 ただし、 \frac{g'(z)}{g(z)} は C の上と内部で正則なので、 Cauchy の定理より積分値が 0 となる。
一方、 f による C の像 w=f(C(t)) を考えればこれも複素平面上の閉曲線で、積分の変換公式を使えば \int_C \frac{f'(z)}{f(z)}dz=\int_{f(C)} \frac{dw}{w}=2\pi\sqrt{-1}n(f(C),0) となる。
よって、回転数についての等式 n(f(C),0)=\sum_{i=1}^n n(C,\alpha_i) が言えた。 さらに、 C が単純閉曲線と仮定しているので、この右辺の n(C,\alpha_i) は全て 1 である。 よって、 n(f(C),0) は C の内部での f の零点の(重複度を込めた)個数である。
関連して、偏角の原理 (the argument principle) を紹介しておく:定理(偏角の原理). C を単純閉曲線とし、複素関数 f は C 上とその内側で有理型関数であるとする。 また、 f は C 上に零点や極を持たないとする。 このとき、次の2つが成り立つ:
- C の内部にある f の零点を a_j, 極を b_k とすると、 \frac{1}{2\pi\sqrt{-1}}\int_C\frac{f'(z)}{f(z)}dz=\sum_j n(C,a_j)-\sum_{k} n(C,b_k). ただし、和は零点の重複度、極の位数を込めて考える。
- C の内部にある f の零点の個数を(重複度を込めて) N, 極の個数を(位数を込めて) P とすると、 \frac{1}{2\pi\sqrt{-1}}\int_C\frac{f'(z)}{f(z)}dz=N-P.
この連載は複素解析入門ではない。 これ以上の詳しいことは複素解析の教科書を参照されたい。
回転数と Sturm 列
回転数を使えば多項式の根の個数が数えられることがわかったが、複素積分はあまり計算に便利ではない。 そこで、別の方法で回転数を計算することを考えよう。 以下、もっぱら原点に関する回転数を考える。
複素平面は、虚軸によって、2つの領域(半平面)に分けられる。 ここで考える曲線は原点を通らないと仮定しているので、虚軸の正の部分と負の部分に「関所」を作れば、曲線は左右の半平面を移動する際に必ず「関所」を通過する。 この「関所」を監視して、その際の向きを数えておけば、曲線が原点の周りを何回まわるかを正確に数えられる。
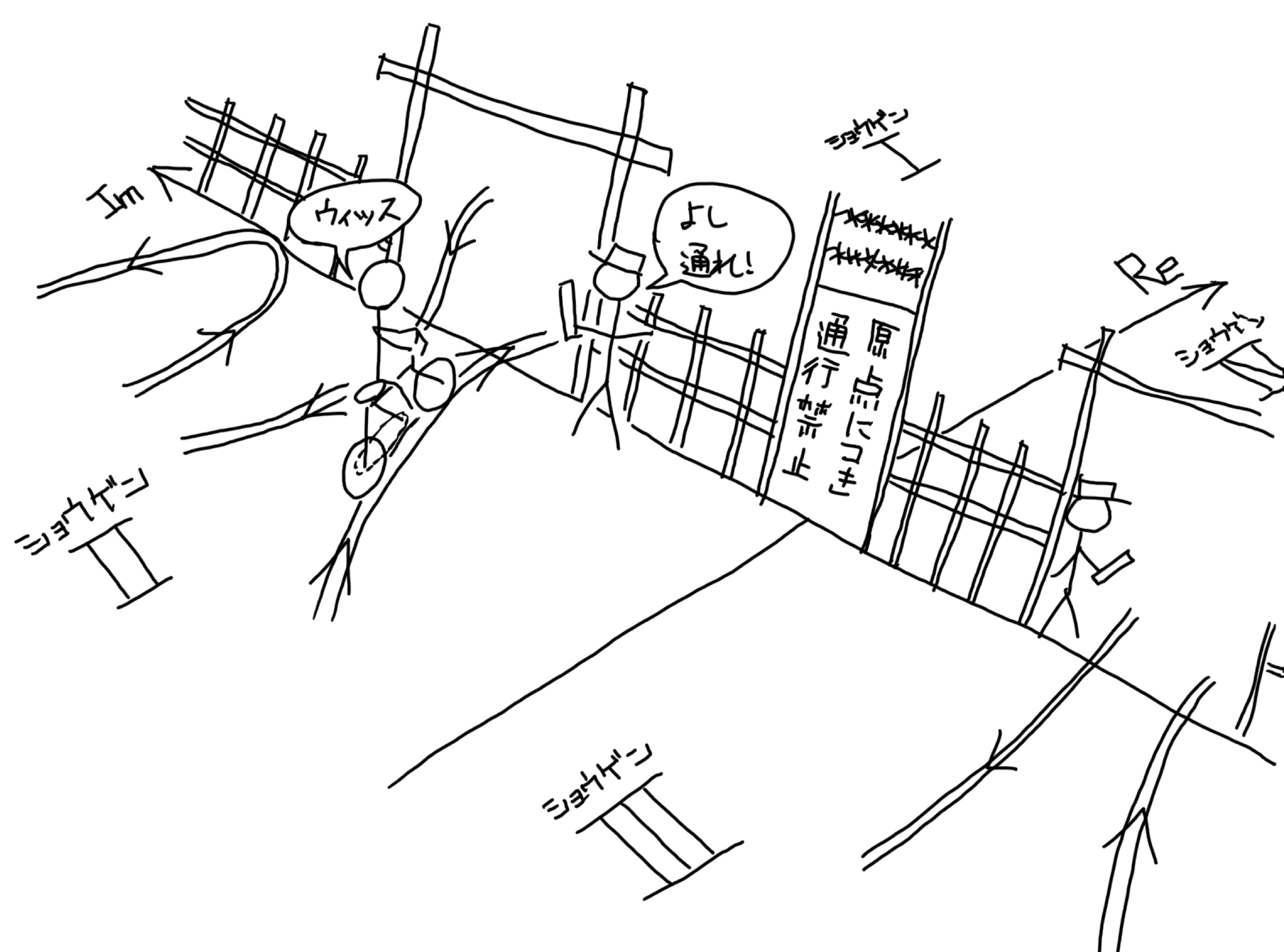
具体的には、 w=C(t) が w 平面の虚軸を通る際に
- 第1象限から第2象限に進む際は(正の向きなので)カウントを +1
- 第2象限から第1象限に戻る際は(負の向きなので)カウントを -1
- 第3象限から第4象限に進む際は(正の向きなので)カウントを +1
- 第4象限から第3象限に戻る際は(負の向きなので)カウントを -1
とすれば、曲線が原点の周りを正の向きに一周するごとにカウントが2増えるので、その総和が回転数の2倍となる。

この方法で、例示した曲線の回転数を数えてみよう。
まず、曲線1は虚軸と4箇所で交わり、いずれも正の向きに進んでいる。 よってカウントの総和は 4 で、回転数はその半分の 2 である。

次に、曲線2は虚軸と6箇所で交わり、正の向きが4箇所、負の向きが2箇所である。 よってカウントの総和は 4-2=2 で、回転数はその半分の 1 である。

曲線3は虚軸と4箇所で交わり、正の向きが2箇所、負の向きが2箇所である。 よってカウントの総和は 2-2=0 で、回転数はその半分の 0 である。

このように、虚軸との交わり方によって回転数を計算できることがわかった。
曲線が多項式で表される場合に回転数を数える方法を、一般 Strum 列を使って表しておこう:定理. C:[t_0,t_1]\to\mathbf{C} を多項式で表される閉曲線とする。 C は原点を通らないと仮定する。 C の実部と虚部をそれぞれ u, v とおく: u(t):=\operatorname{Re}C(t), \quad v(t):=\operatorname{Im}C(t). u, v から始まる一般 Sturm 列を考え、その符号の変化の数を V(u,v;t) とすると、 C の原点の周りの回転数 n(C,0) は、次のように与えられる: n(C,0)=-\frac{1}{2}\sum_{u(t)=0} \chi(u,v;t)=\frac{1}{2}(V(u,v;t_1)-V(u,v;t_0)).
一般 Sturm 列に対して定義した整数 \chi と、回転数を数えるために定義した整数は、符号が逆になっていることに注意されたい。
「C は原点を通らない」と仮定しているが、具体的な曲線 C に対してこの仮定が成り立つかどうかは、 u と v の GCD が実根を持つかどうかをチェックすれば確かめられる。
より一般に、曲線が「区分的に」多項式で表される場合は次のようになる:定理. C_i:[t_{i-1},t_{i}]\to\mathbf{C} を多項式で表される曲線とし、 C=C_1+\cdots+C_l は閉曲線であるとする。 また、 C は原点を通らないと仮定する。 C_i の実部と虚部をそれぞれ u_i, v_i とおく: u_i(t):=\operatorname{Re}C_i(t), \quad v_i(t):=\operatorname{Im}C_i(t). u_i, v_i から始まる一般 Sturm 列を考え、その符号の変化の数を V(u_i,v_i;t) とすると、 C の原点の周りの回転数 n(C,0) は、次のように与えられる: n(C,0)=-\frac{1}{2}\sum_{i=1}^l \sum_{u_i(t)=0} \chi(u_i,v_i;t)=\frac{1}{2}\sum_{i=1}^l (V(u_i,v_i;t_{i})-V(u_i,v_i;t_{i-1})).
回転数というと位相的な量で、代数的な計算はしづらいのではと思うかもしれないが、扱う曲線が多項式や有理関数であれば、一般 Sturm 列を使うことで正確に数えることができるのだ。
これまでのまとめとして、「曲線で囲まれた領域における多項式の根の個数」を与える方法を、定理の形で述べておこう。
系. C\colon[t_0,t_1]\to\mathbf{C} を複素平面の単純閉曲線、 f を複素数係数の多項式とする。 また、 f(C(t)) は多項式であるとする。 このとき、 f(C(t)) の実部と虚部をそれぞれ u(t)=\operatorname{Re}f(C(t)),\ v(t)=\operatorname{Im}f(C(t)) とおくと、 C の内部における f の零点の個数 N は N=n(f(C),0)=\frac{1}{2}(V(u,v;t_1)-V(u,v;t_0)) で与えられる。
しかし、この定理がそのまま利用できるとは限らない。 以下、具体的な領域について、多項式の根の個数を数える方法を考えていこう。
ケース1:半平面における根の個数
まず、半平面における根の個数を考えよう。 実軸で区切られた半平面(上半平面、下半平面)に関して、次の結果が成り立つ:定理. 複素数係数の n 次多項式 f は実根を持たないとする。 実変数 t について f(t) の実部と虚部をそれぞれ、 u と v とおく: u(t)=\operatorname{Re}f(t), v(t)=\operatorname{Im}f(t) u, v から始まる拡張 Sturm 列の符号の変化の数を V とする。 すると、上半平面における(重複を込めた)根の個数 N, 下半平面における(重複を込めた)根の個数 N' は、次で与えられる: N=\frac{1}{2}(n+V(u,v;\infty)-V(u,v;-\infty)),\quad N'=\frac{1}{2}(n+V(u,v;-\infty)-V(u,v;\infty)).

この定理は上半平面と下半平面に関する主張だが、左半平面(実部が負)と右半平面(実部が正)に関するバージョンもあり、それは Routh-Hurwitz の定理と呼ばれている。
(さっきまでの議論では閉曲線を対象としていたのに、この例の境界(実軸)は閉曲線ではない。最初の例なのに!)
証明. 代数学の基本定理より f は重複を込めて n 個の根を持つので、 N+N'=n はわかりきっている。 そこで、上半平面における根の個数が \frac{1}{2}(n+V(u,v;\infty)-V(u,v;-\infty)) であることを確かめれば良い。
f に 0 でない定数をかけても根の位置は変わらないので、 a_n は正の実数と仮定して良い。
まず、根の個数はせいぜい有限個なので、十分大きな実数 R を取ってきて、 f の全ての根を内部に含むような円 \left\lvert z\right\rvert=R を考えることができる。 (R を具体的に与える方法については #2 で「根の限界」として取り扱った。)
この円 \left\lvert z\right\rvert=R の上半分と、実軸の [-R,R] の部分を繋げた曲線 C=c_1+c_2 を考える。 c_1 と c_2 のそれぞれについて積分 \int_{c_1}\frac{f'(z)}{f(z)}dz, \int_{c_2}\frac{f'(z)}{f(z)}dz を考えたい。

まず、半円 c_2 上で、 f は a_nz^n に近似できる。 つまり、 f(z)=a_nz^n(1+h(z)),\quad h(z)=\frac{a_{n-1}}{a_n z}+\cdots+\frac{a_j}{a_n z^{n-j}}+\cdots+\frac{a_0}{a_n z^n} とおいたとき R を十分大きく取れば \left\lvert h(z)\right\rvert をいくらでも小さくでき、 \int_{c_2}\frac{f'(z)}{f(z)}dz\to n\pi\sqrt{-1}\quad(R\to \infty) が成り立つ。
一方、実軸の区間 c_1 に対して、 f(c_1) は f(-R) から f(R) まで移動する。 R が十分大きければ、(a_n が正の実数と仮定したので) f(R) は実軸の正の部分に近く、 f(-R) は(n の偶奇に応じて)実軸の正または負の部分に近い: \begin{gathered} f(R)\approx a_nR^n, \quad f(-R)\approx (-1)^n a_nR^n \\ \arg f(R)\to 0, \quad \arg f(-R)\to\begin{cases}0&n\text{ even}\\\pi&n\text{ odd}\end{cases} \end{gathered} このような状況では、 \int_{c_1}\frac{f'(z)}{f(z)}dz は Sturm 列の符号の変化の数の差 V(u,v;R)-V(u,v;-R) の \pi\sqrt{-1} 倍とほぼ等しくなる。 つまり \int_{c_1}\frac{f'(z)}{f(z)}dz\to \pi\sqrt{-1}(V(u,v;\infty)-V(u,v;-\infty))\quad(R\to\infty) である。
よって、 R\to\infty のとき N=n(f(C),0)=\frac{1}{2\pi\sqrt{-1}}\left(\int_{c_1}\frac{f'(z)}{f(z)}dz+\int_{c_2}\frac{f'(z)}{f(z)}dz\right)\to\frac{n+V(u,v;\infty)-V(u,v;-\infty)}{2} であるが、 N は整数なので等号が成り立ち、 N=\frac{n+V(u,v;\infty)-V(u,v;-\infty)}{2} を得る。
通常の単純閉曲線で囲まれた領域の場合は根の個数は V の差の半分で与えられたが、この定理の N の表し方では、 V の差に、さらに n が加わっている。 これは f が無限遠点 z=\infty で n 位の極を持つことと関連づけて考えることもできそうだが、ここでは深く立ち入らない。
ケース2:円の内部における根の個数
f を複素数係数の n 次多項式とし、中心 z_0, 半径 r の円周上には f の根はないとする。 この時、円の内部にある f の根の個数を知りたい。
まず、中心 z_0, 半径 r の円のパラメーター表示は、 c(t)=z_0+r\cdot\frac{(1-t^2)+2\sqrt{-1}t}{1+t^2}\quad(-\infty\le t\le\infty) で与えられる。

c は多項式ではなく有理関数なので、合成 f(c(t)) も有理関数となるが、 f(c(t)) に (1+t^2)^n を掛ければ多項式となる。 (1+t^2)^n は常に正の実数なので、 f(c(t)) と (1+t^2)^nf(c(t)) の偏角は等しく、特に t を動かした時の回転数も等しい。 よって、 f(c(t)) の代わりに (1+t^2)^n f(c(t)) の回転数を数えれば良い。
というわけで (1+t^2)^n f(c(t)) の実部と虚部をそれぞれ u(t), v(t) とおき、 u, v から始まる Sturm 列の符号の変化の数を V(u,v;t) とする。 u(t)+\sqrt{-1}v(t)=(1+t^2)^n f\Bigl(z_0+r\cdot\frac{1-t^2+2\sqrt{-1}t}{1+t^2}\Bigr)
すると、円の内側における根の個数 N は N=\frac{V(u,v;\infty)-V(u,v;-\infty)}{2} で与えられる。
円のパラメーター表示と言ったら普通は「z_0+re^{i\theta}」という風に指数関数(三角関数)を使うものを思い浮かべるかもしれないが、有理関数でもパラメーター表示ができるというのがポイントである。
ケース3:長方形の内部における根の個数
f を複素数係数の n 次多項式とする。 長方形で囲まれた領域 \{z\mid a<\operatorname{Re}z<b,c<\operatorname{Im}z<d\} に f の根がいくつあるか考えよう。 例によって、長方形の辺の上には f の根はないものとする。

長方形の4つの辺を、それぞれ次のようにパラメトライズする: \begin{aligned} c_1(t_1)&=t_1+\sqrt{-1}c\quad(a\le t_1\le b), \\ c_2(t_2)&=b+\sqrt{-1}t_2\quad(c\le t_2\le d), \\ (-c_3)(t_3)&=t_3+\sqrt{-1}d\quad(a\le t_3\le b), \\ (-c_4)(t_4)&=a+\sqrt{-1}t_4\quad(c\le t_4\le d), \\ \end{aligned}
ただし、 c_3 と c_4 は、曲線上を進むにつれてパラメーター t が減るようにパラメトライズする。
長方形の周は、これらの和となる: C=c_1+c_2+c_3+c_4
それぞれの辺について
- f(c_1(t_1))=f(t_1+\sqrt{-1}c) の実部 u_1 と虚部 v_1 から始まる Sturm 列を考え、その Sturm 列の符号の変化の数を V(u_1,v_1;t_1) とする。
- f(c_2(t_2))=f(b+\sqrt{-1}t_2) の実部 u_2 と虚部 v_2 から始まる Sturm 列を考え、その Sturm 列の符号の変化の数を V(u_2,v_2;t_2) とする。
- f(c_3(t_3))=f(t_3+\sqrt{-1}d) の実部 u_3 と虚部 v_3 から始まる Sturm 列を考え、その Sturm 列の符号の変化の数を V(u_3,v_3;t_3) とする。
- f(c_4(t_4))=f(f(a+\sqrt{-1}t_4)) の実部 u_4 と虚部 v_4 から始まる Sturm 列を考え、その Sturm 列の符号の変化の数を V(u_4,v_4;t_4) とする。
この時、 N=\frac{1}{2}\left( \begin{aligned} &V(u_1,v_1;b)-V(u_1,v_1;a) +V(u_2,v_2;d)-V(u_2,v_2;c) \\ &\quad+V(u_3,v_3;a)-V(u_3,v_3;b) +V(u_4,v_4;c)-V(u_4,v_4;d) \end{aligned} \right) が長方形の内側における根の個数を与える。
予定では今回が(とりあえずの)最終回となるはずだったが、「虚根の分離」のトピックが予想外に重かったため、ここで一区切りとする。 次回こそは、虚根の分離と、代数的数の実装を行いたい。
参考文献
- L.V. Ahlfors, Complex Analysis, 3rd. ed., McGraw-Hill, 1979.
- 複素解析の定番教科書。邦訳もある。
- 高木貞治 著「代数学講義 改訂新版」共立出版、1965年
- P. Henri, Applied and Computational Complex Analysis. Vol. 1. Power Series-Integration-Conformal Mapping-Location of Zeros, John Wiely & Sons, 1974.
- S. Basu, R. Pollack, M.-F. Roy, Algorithms in Real Algebraic Geometry, 2nd. ed., Springer, 2006.
- J.R. Pinkert, An Exact Method for Finding the Roots of a Complex Polynomial, TOMS, Vol. 2, No. 4, pp351-363, 1976
- H.S. Wilf, A Global Bisection Algorithm for Computing the Zeros of Polynomials in the Complex Plane, JACM, Vol. 25, No. 3, pp415-420, 1978
- G. E. Collins and W. Krandick, An Efficient Algorithm for Infallible Polynomial Complex Roots Isolation, In Proceedings of ISSAC ’92, pp189-194, ACM, 1992
- M.A.O. Camargo Brunetto, D.M. Claudio, and V. Trevisan, An Algebraic Algorithm to Isolate Complex Polynomial Zeros Using Sturm Sequences, Computers & Mathematics with Applications, Vol. 39, pp95-105, 2000