#0 イントロダクション

はじめに：計算機で扱える実数（よもやま話）

計算機で実数を扱うと言った時、皆さんはどのようなものを思い浮かべるだろうか。

少しでもプログラミングをやったことのある方ならご存知の通り、計算機で実数を扱う際は浮動小数点数を使うことが多いと思う。 しかし、浮動小数点数は単なる近似であり、誤差がつきまとう。 例えば、広く使われている2進倍精度（精度53ビット）の浮動小数点数では、 0.1 + 0.1 + 0.1 と 0.3 は同じ値にならない。

では、実数を正確に計算するにはどうしたら良いだろうか？ 浮動小数点数でも近似の桁数を増やせば誤差は減る。 とすると、数の計算方法を覚えておいて、必要になったら必要な精度で計算するというのはどうか？

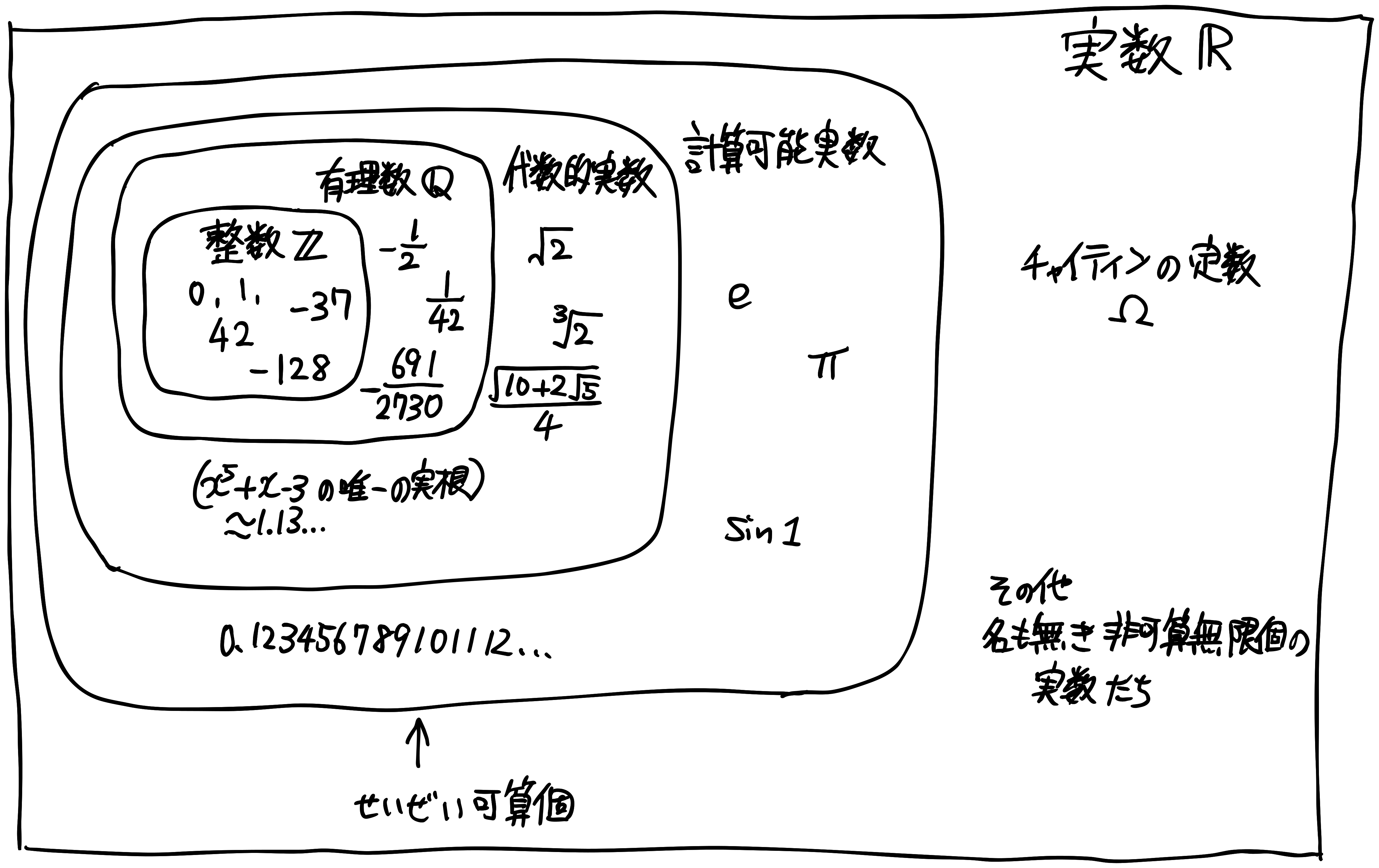
このアイディアを精密化したものが「計算可能実数」である。 我々が扱うほとんどの実数、 \(\sqrt{2}\), \(e\), \(\pi\) 及びその四則演算、実数上の有名な関数の多く（初等関数など）は計算可能である。

（とはいえ、計算可能な関数はせいぜい可算個しかないので、計算可能実数は実数全体のほんの一部でしかない。 具体的に「計算可能でない実数」を挙げるとすれば、「（特定のプログラミング言語で書いた）プログラムが停止する確率」であろう→「チャイティンの定数」で検索）

計算可能実数は万能に見えるが、しかし、重大な欠点がある。 計算可能実数同士の比較演算、特に「等しいかどうか」は計算可能ではない。 直感的だが不正確な言い方をすれば、「2つの計算可能実数が等しいかどうか判断するには、数の全ての桁を調べる必要があるが、有限時間でそれはできない」となるだろうか。 より厳密な説明は、適切な文献（参考文献4など）を参照してほしい。

少し話を後退させよう。 「比較演算も含めて決定可能な」実数の部分集合にはどのようなものがあるだろうか？

まず、整数 \(\mathbb{Z}\) は、多倍長計算を駆使すれば、何桁であっても計算機上で正確に取り扱える。 C言語であれば自力で実装するかGMPなどのライブラリーを使って多倍長計算を行うことになるが、プログラミング言語によっては、特に意識せずに多倍長整数を使えるものもある。

次に、有理数 \(\mathbb{Q}\) は、整数2つの組で表せるので、計算機上で正確に取り扱える。 これもプログラミング言語によっては標準で用意されていたりする。

有理数の有限次代数拡大も良さそうだ。 例えば、 \(\mathbb{Q}(\sqrt{2})\) であれば \(x+y\sqrt{2}\) を有理数2つの組 \((x,y)\in\mathbb{Q}^2\) として表せば良い。 \(\mathbb{Q}(\sqrt{2})\) の演算は、組 \((x,y)\) に対する演算として実装できる。

さらに言うと、有理数の代数閉包 \(\overline{\mathbb{Q}}\) 、すなわち代数的数も、計算機で正確に取り扱える。 ここでは実数の部分集合についての話をしているから、それに合わせるならば、「代数的実数は計算機で正確に取り扱える」となるだろう。

残念ながら \(e\) や \(\pi\) は代数的でない（超越数）。 超越数もある程度取り扱いたい場合は…筆者の力量を超えるので、参考文献4「周期と実数の0-認識問題 Kontsevich-Zagier の予想」を参照して欲しい。

ともかく、代数的実数というのは、四則演算、平方根や立方根などの操作（もっと一般に、有理数係数多項式の実根を取る操作）、そして比較演算が不自由なく行える体系である。 「計算機における実数」という観点でのマイルストーンとして、掘り下げる価値はあるだろう。 そこで、これから何回かに分けて、計算機における代数的実数の実装方法を述べることにする。

（ちなみに、平方根さえ取れれば良い、つまり立方根や一般の多項式の実根を取る操作が必要ないのであれば、「作図可能な数」を実装するという手もある）

基本的な方針：代数的実数の表し方

代数的実数は、整数係数多項式の根(こん)となる実数である。 具体的な代数的実数を取り扱う上では、それを根(こん)に持つ多項式が重要である。 （このような多項式のうち次数が最小のものを、最小多項式 (minimal polynomial) という。代数的数を根に持つ多項式は、その最小多項式で割り切れる。）

多項式は一般に複数の根を持つため、表したい代数的実数が多項式の根のうちのどれであるかを、何らかの方法で指示しなくてはならない。 指示の方法としては、「小さいものから数えて \(k\) 番目」とするか、あるいは根を分離できるような十分狭い区間を使う（\(\sqrt{2}\) であれば「\(x^2-2\) の1以上2以下に存在する唯一の根」という感じ）方法がある。 ここでは後者を使うことにする。 （大雑把な大きさがわかっていると、他の代数的実数と大小関係を比較する際に有利である。）

つまり、1つの代数的実数を表すために

• 最小多項式 \(f\) および
• 有理数の区間 \(I\) （ただし、この区間の中に \(f\) の根がちょうど1個だけ存在する）

を使う。 この組 \((f, I)\) について、加減乗除、比較、平方根などの演算を実装していけば良い。

各種アルゴリズムに関しては、まずは遅くてもいいから素朴な方法で実装し、筆者の余力があったらより洗練された方法を紹介することにする。

実装に使うプログラミング言語

その辺のプログラミング言語で扱える整数は、32ビットとか64ビットとかの固定長であることが多い。 しかし、整数および有理数の正確な取り扱いにはこれでは不足で、多倍長計算を行う必要がある。

多倍長計算はもちろん自力で実装することもできるし、外部のライブラリーを利用することもできるが、準備の手間を考えると、なるべく言語の標準ライブラリーで提供されていることが望ましい。 また、有理数も、多倍長整数があれば自分で実装することはできるが、標準ライブラリーで提供されていた方が楽である。

多倍長整数と有理数を、組み込み型あるいは標準ライブラリーで提供している言語で、筆者の知っているものをいくつか挙げてみる：

• Python (fractions module)
• Ruby (Rational クラス)
• Scheme
• Julia (Arbitrary Precision Arithmetic, Rational Numbers)
• Haskell (Integer 型、 Rational 型)
• OCaml (Module Num)
• Go (math/big)
  • 演算子オーバーロードがない。

標準で多倍長整数はあるが有理数はない言語も、参考までにいくつか挙げておく：

• Java (java.math.BigInteger)
  • 演算子オーバーロードがない。
• Scala (scala.math.BigInt)
• C#, F# (System.Numeric.BigInteger)
• D (std.bigint)

多倍長整数があれば有理数演算の実装は比較的楽なので、これらの言語で実装してみるのも良いだろう。

それ以外に、静的型付き言語で考慮すべき点として、多相（ジェネリクスともいう）の有無がある。 今後、第一級の対象として多項式を扱うことになるが、その際の係数は、整数、有理数、有限体、多項式など、様々である。 多相があれば、多項式に関する操作を係数環ごとに書かなくても、同じコードを使い回せるので、楽ができると見込まれる。 （とはいっても、型クラスのような機構を備えていないと、なんだかんだでコードが冗長になりそうな気もするが……。）

さて、ここで例示するコードであるが、筆者の好みで Haskell を使うことにする。 計算のアルゴリズムはソースコードとは独立に説明するつもりなので、他の言語でも同様に実装できるだろう。 リクエストがあれば、（あるいはネタ切れを起こしたら）他の言語に移植するかもしれない。

Haskellについて

Haskell のセットアップ方法はここでは扱わない。 適切な参考書を参照して欲しい。

筆者のブログに書いたように、 Haskell の Prelude にある Num クラス（およびその仲間たち）はお世辞にも洗練されているとは言えない。 Num クラスを騙し騙し使う、クラス階層を自作する、algebra / algebraic-prelude などを使う、などのやり方があるだろう。 当面は Num クラスを使うことにする。

モジュールの名前は Numeric.AlgebraicReal.* を使うことにする。stack でのセットアップ例：

$ stack new algebraic-real simple-library
$ cd algebraic-real
$ tree
.
├── LICENSE
├── README.md
├── Setup.hs
├── algebraic-real.cabal
├── src
│   └── Lib.hs
└── stack.yaml

1 directory, 6 files
$ mkdir -p src/Numeric/AlgebraicReal

必要な知識

少なくとも、大学1,2年程度の代数は必要だろう。 有限体もそのうち使うことになるかもしれない。

参考文献

1. Joachim von zur Gathen and Jürgen Gerhard, Modern Computer Algebra, Third Edition, Cambridge University Press, 2013
   • 分厚い。
   • 代数に関するアルゴリズムを手広く扱っている。
   • 邦訳もあるようだが値段が（3倍くらい）高めで、古い。買うなら原著だろう。
2. Donald E. Knuth 著「The Art of Computer Programming Volume 2 Seminumerical Algorithms Third Edition 日本語版」アスキードワンゴ、2015年
   • 分厚い。
   • 多項式の除算や因数分解を扱っている。
   • Knuthの同名の本の邦訳。
3. 穴井宏和、横山和宏 著「QEの計算アルゴリズムとその応用　数式処理による最適化」東京大学出版会、2011年
   • 代数的実数について扱っている。
4. 吉永正彦 著「周期と実数の0-認識問題 Kontsevich-Zagier の予想」数学書房、2016年
   • 「代数的実数よりも広くて、比較演算が決定可能な数のクラス」の候補である周期がテーマである。
   • 代数的実数や、計算可能実数の等号認識問題が計算不可能である件も扱っている。

• 目次
• 次：#1 一変数多項式環