#16 虚根の数え上げ、そして代数閉体へ(後編)
虚根の数え上げ:境界上に根がある場合
虚根を数える際、前回は「曲線 C の上に根はない」と仮定したが、そもそも根の位置がわからないので、この仮定が成り立つことは事前にはわからない。 もちろん、具体的な多項式と曲線が与えられた時にこの仮定が成り立つかどうかを確かめることはできる。 曲線 C が f の実根を通ることと、 f(C(t)) が実根を持つことは同値なので、 f(C(t)) が実根を持つか確認すれば良い。
f が実根 \alpha=C(\tau) を持っていた場合に取るべき行動としては、3通り考えられる:
- f(x) を x-\alpha で割ったもの f(x)/(x-\alpha) についてアルゴリズムを続行する
- C を「ちょっとずらした」もの C' について根の数え上げを実行する。C' は f の根を通らないことが期待される。
- C が f の根を通る場合でもうまく動くアルゴリズムを考える。
1. はシンプルな方法だが、もとの多項式 f(x) が整数係数であっても、 x-\alpha で割ったものは係数が代数的実数になってしまう。 代数的実数を係数とする多項式はなるべく扱いたくないので、 1. はできれば避けたい。
2. ではせっかく計算した関数合成 f(C(t)) を破棄して別の関数合成 f(C'(t)) を試すことになる。 (大したコストではないと思うが)
というわけで、ここでは 3. を考えたい。
虚軸との交差
前回、「閉曲線と虚軸との交わりを符号付きで数えることで原点周りの回転数を計算できる」ということを見た。 今回、「閉じているとは限らない」曲線について、虚軸との交わりを考えたい。
考えたい概念に対して名前と記号があると便利なので、導入しよう。 C\colon[a,b]\to\mathbf{C}\setminus\{0\} は原点を通らない連続な曲線であって、虚軸と交差する点(実部が0になる点)は有限個であるとする。 このとき、交差数 \operatorname{Cross}(C) または \operatorname{Cross}(C;a,b) (写像度の周辺で似たような概念が登場するようだが、この「交差数」はこの連載独自の用法である)を、次のように定める:
C(t) の実部が 0 となる t を a\le t_1<t_2<\cdots<t_n\le b とおく。 各 t_i について、整数 \psi_{\mathrm{in}} と \psi_{\mathrm{out}} を次のように定める。
- C が第2象限から虚軸の正の部分へ「入ってくる」とき、\psi_{\mathrm{in}}(C;t_i)=-1
- C が第4象限から虚軸の負の部分へ「入ってくる」とき、\psi_{\mathrm{in}}(C;t_i)=-1
- それ以外の場合、 \psi_{\mathrm{in}}(C;t_i)=0
- C が虚軸の正の部分から第2象限へ「出て行く」とき、\psi_{\mathrm{out}}(C;t_i)=+1
- C が虚軸の負の部分から第4象限へ「出て行く」とき、\psi_{\mathrm{out}}(C;t_i)=+1
- それ以外の場合、 \psi_{\mathrm{out}}(C;t_i)=0

この時、 \operatorname{Cross}(C)=\operatorname{Cross}(C;a,b) :=\sum_{\begin{array}{c}\scriptstyle 1\le i\le n,\\\scriptstyle a<t_i\le b\end{array}} \psi_{\mathrm{in}}(C;t_i) +\sum_{\begin{array}{c}\scriptstyle 1\le i\le n,\\\scriptstyle a\le t_i<b\end{array}} \psi_{\mathrm{out}}(C;t_i) と定める。
\operatorname{Cross}(C) は、 C の端点が虚軸の上に載っていたり、 C が途中で虚軸に接していても、問題なく定義できるのがポイントである。 (前回触れた Cauchy 指数は、端点が極でないことを仮定していた)
交差数の性質をいくつか確認しておこう。
交差数は曲線の連結について加法性を満たす: \operatorname{Cross}(C_1+C_2)=\operatorname{Cross}(C_1)+\operatorname{Cross}(C_2).
曲線が閉曲線の場合、交差数は、原点周りの回転数の2倍となる: 2n(C,0)=\operatorname{Cross}(C)
C が多項式で表される場合は、交差数を一般 Sturm 列を使って計算できる:定理. C が多項式で表される曲線 C(t)=u(t)+\sqrt{-1}v(t) の場合は \operatorname{Cross}(C;a,b)=V(u,v;a)-V(u,v;b).
C\colon[a,b]\to\mathbf{C}\setminus\{0\} に、符号一定な連続関数 g\colon[a,b]\to\mathbf{R}\setminus\{0\} をかけても交差数は変わらない: \operatorname{Cross}(gC)=\operatorname{Cross}(C).
境界上に根がある場合の実根の数え上げ
問題: 単純閉曲線 C=c_1+c_2+\cdots+c_l で囲まれた領域における、多項式 f の根の個数を考えたい。 各 c_i が f の根を通っていても良いが、各 c_i の端点は f の根ではないと仮定する。 C で囲まれた領域の内部の根の個数を考え、境界 C 上の根は数えない。
(C 上も含めた根の個数を数えたい場合は、まず C の内部の根の個数を数え、それに C 上の根の個数を加えれば良い。)
例えば、次の図中の × 印を f の根、太い曲線を曲線 C とする。 C の上に f の根が5個重なっているが、それらは無視して、 C の内部にある根の個数(3個)を数えたい。

以後、曲線 C の f による像を F(t)=f(C(t)), 各部分を F_i(t)=f(c_i(t)) とおく。 問題としては「曲線 F の原点周りの回転数を計算したい」とでも言えそうだが、 F は原点を通るかもしれないのでその言い方は正しくない。
なお、多項式 f と曲線 C について、
- f は重根を持たない。
- 各成分 c_i の微分は消えない(つまり、常に c_i'(t)\ne 0 となる)。
と仮定する。 この時、 F_i'(t)=\frac{d}{dt}f(c_i(t))=f'(c_i(t))c_i'(t) より、 F(t) の実根 t=\tau で F(t) の微分が消えないこと F'(\tau)\ne0 が言える。
このままでは前回の議論が使えないので、曲線 C を、 f の根を通らないように「修正」することを考える。 具体的には、 C 上にある f の根 \alpha それぞれに対して、 \alpha を中心とする小さな円を描く。 そして、もともと根 \alpha を通っていた部分を、今描いた円に沿って「迂回」させる。 円周上を動く向きは負の向き(反時計回り)である。 そうやって「修正」した曲線を \tilde{C}=\tilde{c}_1+\cdots+\tilde{c}_l とし、 \tilde{F}(t)=f(\tilde{C}(t)), \tilde{F}_i(t)=f(\tilde{c}_i(t)) とおく。
さっき例示した曲線を「修正」したものを、次に図示する:

計算したいのは \tilde{C} の内部にある f の根の数であり、 \tilde{F}=f(\tilde{C}) の回転数、あるいは交差数である。 しかし、 \tilde{C} は、幾何学的な意味は明瞭だが、計算には向かない。 そこで、もっと計算に向いた量を考えよう。
F_i(t) が実根を持つということは、 \operatorname{Re}F_i, \operatorname{Im}F_i の GCD g_i:=\gcd(\operatorname{Re}F_i,\operatorname{Im}F_i) が定数でないということである。 このとき、 F_i の代わりに F_i^*=F_i/g_i を考えれば F_i^* は実根を持たないので、一般 Sturm の定理によって交差数を計算できる。
こうして、F_i を基にした、「原点を通らない」2種類の曲線 \tilde{F}_i, F_i^* が得られた:
- \tilde{F}_i: 幾何学的意味は明らかだが、計算はしづらい。
- F_i^*: 計算はしやすいが、幾何学的意味は明らかではない。
この2種類の曲線がどう関連しているか見ていこう。 簡単のため、各 F_i は虚軸と高々1回しか交わらないとする。 はじめに与えられた曲線がこの仮定を満たさなくても、必要に応じて曲線を細かく分割すれば、この仮定を満たすようにできる。
まず、 F_i が原点を通らない場合を確認しよう。 この区間で C に対する「修正」は必要ないので \tilde{F}_i=F_i である。 また、 g_i は符号一定なので、 \operatorname{Cross}(\tilde{F})=\operatorname{Cross}(F^*) である。
次に、 F_i が t=\tau において原点を通る場合を考えよう。 g_i は重根を持たないので、 t=\tau の前後で符号が変化する。 t<\tau のとき g(t)<0, t>\tau のとき g(t)>0 と仮定しても一般性を失わない。
- F_i は次の図のように原点を通って虚軸の反対側へ向かう場合を考える。 f は正則なので、\tilde{F}_i は、負の方向に回転して原点を迂回する。 一方、 F_i^* は虚軸に関してずっと同じ側にいる。 よって、 \operatorname{Cross}(\tilde{F}_i)=-1, \operatorname{Cross}(F_i^*)=0 である。

- F_i が第4象限から原点を通って第1象限に向かう場合を考える。 \tilde{F}_i はやはり、負の方向に回転して原点を迂回する。 一方、 F_i^* は第2象限から第1象限へ移動する。 よって、 \operatorname{Cross}(\tilde{F}_i)=-2, \operatorname{Cross}(F_i^*)=-1 である。

- F_i が第1象限から原点を通って第4象限に向かう場合を考える。 \tilde{F}_i はやはり、負の方向に回転して原点を迂回する。 一方、 F_i^* は第3象限から第4象限へ移動する。 よって、 \operatorname{Cross}(\tilde{F}_i)=0, \operatorname{Cross}(F_i^*)=+1 である。

i. ii. iii. のいずれの場合も、次の関係式が成り立つ: \operatorname{Cross}(\tilde{F}_i)=\operatorname{Cross}(F_i^*)-1.
F_i が原点を通る場合というのは、 i. ii. iii. のいずれかの場合に該当する。 あるいは、 F_i が原点に接触して同じ象限に戻って行く場合というのは(F_i の微分が消えないという仮定より)あり得ないので、考えなくても良い。
結局、次の結果を得る: g_i の実根の個数を m_i とすると、 \operatorname{Cross}(\tilde{F}_i)=\operatorname{Cross}(F_i^*)-m であり、 F 全体で考えると、和を取って \operatorname{Cross}(\tilde{F})=\sum_i \left(\operatorname{Cross}(F_i^*)-m_i\right) となる。
有理曲線と有理関数の場合
f が有理関数の場合も考えよう。 ただし、 f の零点や極の位数(重複度)は高々1と仮定する。 引き続き、 C=c_1+\cdots+c_l の各 c_i の端点は f の零点でも極でもないと仮定していく。
例によって F_i=f(c_i) とおき、 F_i は F_i(t)=f(c_i(t))=\frac{p_i(t)(u_i(t)+\sqrt{-1}v_i(t))}{q_i(t)} という風に有理関数で書けるとする。 ただし u_i,v_i\in\mathbf{R}[t] は互いに素、 p_i,q_i\in\mathbf{R}[t] は互いに素とする。 この時、 F_i^*(t)=u_i(t)+\sqrt{-1}v_i(t) とおく。
まず、 C 上に f の零点や極がない場合は、偏角の原理より、回転数 n(f(C),0) は「C の内部にある零点の個数 N と極の個数 P の差」を与える: \operatorname{Cross}(f(C))=n(f(C),0)=2(N-P).
だが、 C 上に f の零点や極があると、曲線 C を修正する必要がある。 修正の方法としてはやはり、 f の零点や極を内側に迂回するようにする。
零点を迂回した場合は、修正した曲線 \tilde{C} の像 f(\tilde{C}) は、原点を負の向きに回ることになる。
一方、極を迂回した場合は、 f(\tilde{C}) は、原点の遠くを、正の向きに回って迂回することになる。 向きが逆になるので、 \operatorname{Cross}(\tilde{F}_i) と \operatorname{Cross}(F_i^*) の差の符号は(零点の場合とは)逆になり、極1個につき \operatorname{Cross}(\tilde{F}_i)=\operatorname{Cross}(F_i^*)+1 となる。
まとめると、 p_i の実根の個数(F_i の零点の個数)を m_i、 q_i の実根の個数(F_i の極の個数)を n_i とすると、 \operatorname{Cross}(\tilde{F}_i)=\operatorname{Cross}(F_i^*)-(m_i-n_i) であり、 F 全体で考えると、和を取って \operatorname{Cross}(\tilde{F})=\sum_i \left(\operatorname{Cross}(F_i^*)-(m_i-n_i)\right) となる。
C 上にある f の零点や極の位数が2以上の場合にも一般化できそうな気がするが、ここではしないでおく。
実装
今回のモジュール名は Numeric.AlgebraicReal.AlgNum とし、ファイル名は src/Numeric/AlgebraicReal/AlgNum.hs とする。
お決まりの import 文を書いていく:
module Numeric.AlgebraicReal.AlgNum where
import Numeric.AlgebraicReal.Class
import Numeric.AlgebraicReal.UniPoly
import Numeric.AlgebraicReal.Resultant
import Numeric.AlgebraicReal.AlgReal
import Numeric.AlgebraicReal.Interval
import Numeric.AlgebraicReal.CReal
import Numeric.AlgebraicReal.Complex
import Numeric.AlgebraicReal.Factor.SquareFree
import Numeric.AlgebraicReal.Factor.Hensel
import System.IO.Unsafe (unsafePerformIO)
import qualified Data.Vector as V
import Data.List
import Data.Ratio虚根の数え上げ
まずは「与えられた多項式が指定された領域にいくつの根を持つか」を実装しよう。
多項式 f と、多項式によってパラメーター表示された曲線 c から、合成 F(t)=f(c(t)) を計算し、実部と虚部の GCD g=\gcd(\operatorname{Re}F,\operatorname{Im}F) と、 F をそれで割ったもの F^*=F/g の Sturm 列を返す関数 negativePRSOnPath を用意しておく。
曲線 c は、\mathbf{Q}(\sqrt{-1}) 係数の多項式を使って表す。 ただし、なるべく整数係数多項式でやっていきたいので、 c\in\mathbf{Z}[\sqrt{-1}][t] と d\in\mathbf{Z}[\sqrt{-1}] を引数とし、 c/d\in\mathbf{Q}(\sqrt{-1})[t] と表すこととする。
negativePRSOnPath :: UniPoly (Complex Integer) -> UniPoly (Complex Integer) -> Complex Integer -> ([UniPoly Integer], UniPoly Integer)
negativePRSOnPath f c d = (s, uv)
where
fc = fst $ homogeneousCompP f c d
u = mapCoeff realPart fc
v = mapCoeff imagPart fc
uv = gcdD u v
u' = u `divide` uv
v' = v `divide` uv
s | degree u' > degree v' = negativePRS u' v'
| otherwise = u' : negativePRS v' (-u')前回、何種類かの領域について根の数え上げを考えていたが、今回実装するのは長方形領域のみとする。
長方形領域は Complex Interval 型によって表すことにする。
長方形領域の境界は、実軸と平行な(水平な)直線および、虚軸と平行な(垂直な)直線である。 そのため、 negativePRSOnPath をそういう直線に特化したものを用意しておく:
-- c(t) = t + k * sqrt (-1)
negativePRSOnHorizontalLine :: UniPoly (Complex Integer) -> Rational -> ([UniPoly Integer], UniPoly Integer)
negativePRSOnHorizontalLine f k = negativePRSOnPath f (scaleP (fromReal q) ind + constP (fromImag p)) (fromReal q)
where p = numerator k
q = denominator k
-- c(t) = k + t * sqrt (-1)
negativePRSOnVerticalLine :: UniPoly (Complex Integer) -> Rational -> ([UniPoly Integer], UniPoly Integer)
negativePRSOnVerticalLine f k = negativePRSOnPath f (constP (fromReal p) + scaleP (fromImag q) ind) (fromReal q)
where p = numerator k
q = denominator kいよいよ、「与えられた長方形にいくつ根があるか」数える関数 countRootsInRectangle を実装する。
その前に、長方形の周にある根をどう扱うかの仕様を考えておく。 利用シーンとしては、「長方形の周も含めた部分」の根を数えたい場合と、「長方形の上と右の辺(と右上の頂点)を含み、他の辺(と他の頂点)は含まない部分」の根を数えたい場合、両方が考えられる。 そこで、 Bool 型の引数で、左と下の辺を含むかどうか切り替えられるようにしておく。
根を数える多項式 f は整数係数とする。 長方形は、有理数を端点とする2つの区間を使って [a,b]+\sqrt{-1}[c,d] という形で与える。
実際のアルゴリズムだが、
- 長方形の四隅 \{a+c\sqrt{-1},b+c\sqrt{-1},a+d\sqrt{-1},b+d\sqrt{-1}\} が f の根であるかをチェックする。 \alpha\in\{a+c\sqrt{-1},b+c\sqrt{-1},a+d\sqrt{-1},b+d\sqrt{-1}\} が f の根であった場合は、 f を x-\alpha で割ったものを改めて f と置き直す(コード中では
frと置いている)。 四隅のうちいくつが根であったかという整数を、「左と下の辺を含むかどうか」も考慮しつつ、corners変数に入れておく。- f が次数が3以上の(整数係数)既約多項式であれば、長方形の四隅(実部、虚部ともに有理数)が根となることはないので、ここの処理は省略できるだろう。 しかしここでは省略しないでおく。
- 長方形の4辺 c_1,c_2,c_3,c_4 について、 F_i(t)=f(c_i(t)) を計算する。 先述の
negativePRSOnPath関数(の亜種)により、 g_i=\gcd(\operatorname{Re}F_i,\operatorname{Im}F_i) と、\operatorname{Re}F_i/g_i,\operatorname{Im}F_i/g_i から始まる Sturm 列s1,s2,s3,s4を計算する。 - 長方形の4辺上にある f の根の数を数える。 これは g_i の実根の個数を数えれば良い。 数えた結果を
onBottomEdge,onRightEdge,onTopEdge,onLeftEdgeという変数に入れておく。 - 「長方形の内部にある実根の個数」(の2倍)を数える。 つまり、 F_i^* の符号の変化の数を数え、それに「長方形の4辺上にある f の根の数」を足し引きする。 「辺も含む」場合は、 iii. で求めた根の数を全て足す。 「右と上の辺は含むが、左と下の辺を含まない」場合は、
onRightEdge,onTopEdgeを足し、onBottomEdge,onLeftEdgeを引く。 この量をtotalVariationとおく。 totalVariationを2で割ったものとcornersの和が、求めたい根の数である。
という風になる。 コードはやや冗長となった:
countRootsInRectangle :: UniPoly Integer -> Complex Interval -> Bool -> Int
countRootsInRectangle f rect includeLeftAndBottomEdges
| a == b && c == d = if atTopLeft then 1 else 0
| a == b = onRightEdge + (if atTopRight then 1 else 0) + (if atBottomRight then 1 else 0)
| c == d = onTopEdge + (if atTopLeft then 1 else 0) + (if atTopRight then 1 else 0)
| otherwise = (totalVariation `div` 2) + corners
where
Iv a b = realPart rect
Iv c d = imagPart rect
-- 4隅に根をもたないようにする
bottomLeft = MkComplex a c
bottomRight = MkComplex b c
topLeft = MkComplex a d
topRight = MkComplex b d
atBottomLeft = valueAt bottomLeft (mapCoeff fromInteger f) == 0
atBottomRight = valueAt bottomRight (mapCoeff fromInteger f) == 0
atTopLeft = valueAt topLeft (mapCoeff fromInteger f) == 0
atTopRight = valueAt topRight (mapCoeff fromInteger f) == 0
cornerFactors = product [ if atBottomLeft then complexLinearFactor bottomLeft else 1
, if atBottomRight then complexLinearFactor bottomRight else 1
, if atTopLeft then complexLinearFactor topLeft else 1
, if atTopRight then complexLinearFactor topRight else 1
]
-- 4隅にある根の数
corners = length $ filter id [ includeLeftAndBottomEdges && atBottomLeft
, includeLeftAndBottomEdges && atBottomRight
, includeLeftAndBottomEdges && atTopLeft
, atTopRight
]
fr :: UniPoly (Complex Integer) -- f から、長方形の4隅の根を取り除いたもの
fr = mapCoeff fromReal f `divide` cornerFactors
g1, g2, g3, g4 :: UniPoly Integer
s1, s2, s3, s4 :: [UniPoly Integer]
(s1,g1) = negativePRSOnHorizontalLine fr c
(s2,g2) = negativePRSOnVerticalLine fr b
(s3,g3) = negativePRSOnHorizontalLine fr d
(s4,g4) = negativePRSOnVerticalLine fr a
onBottomEdge = countRealRootsBetweenZQ a b g1
onRightEdge = countRealRootsBetweenZQ c d g2
onTopEdge = countRealRootsBetweenZQ a b g3
onLeftEdge = countRealRootsBetweenZQ c d g4
varOnBottomEdge = varianceAtZQ b s1 - varianceAtZQ a s1
varOnRightEdge = varianceAtZQ d s2 - varianceAtZQ c s2
varOnTopEdge = varianceAtZQ a s3 - varianceAtZQ b s3
varOnLeftEdge = varianceAtZQ c s4 - varianceAtZQ d s4
rootsOnEdges = onRightEdge + onTopEdge - negateIf includeLeftAndBottomEdges (onBottomEdge + onLeftEdge)
totalVariation = varOnBottomEdge + varOnRightEdge + varOnTopEdge + varOnLeftEdge + rootsOnEdges
-- @complexLinearFactor z@ は、 @ind - z@ の分母を払ったもの
complexLinearFactor :: Complex Rational -> UniPoly (Complex Integer)
complexLinearFactor (MkComplex x y) = let m = lcm (denominator x) (denominator y)
x' = numerator (x * fromInteger m)
y' = numerator (y * fromInteger m)
in scaleP (fromInteger m) ind - constP (MkComplex x' y')
negateIf :: Num a => Bool -> a -> a
negateIf True = negate
negateIf False = id代数的数の基本的な演算
代数的数 (algebraic number) を表すデータ型の名前は AlgNum とし、実数を表す FromReal データ構築子と、一般の代数的数を表す AlgNum データ構築子を用意する。 最小多項式を返す関数は definingPolynomialN, 分離領域(長方形)を返す関数は isolatingRectangle とする。
data AlgNum = FromReal !AlgReal
| AlgNum !(UniPoly Integer) !(Complex Interval)
deriving (Show)
definingPolynomialN :: AlgNum -> UniPoly Integer
definingPolynomialN (FromReal x) = primitivePart (definingPolynomial x)
definingPolynomialN (AlgNum f _) = f
isolatingRectangle :: AlgNum -> Complex Interval
isolatingRectangle (FromReal x) = MkComplex (isolatingInterval' x) 0
isolatingRectangle (AlgNum _ r) = r代数的数、つまり AlgNum 型の値を作る関数を mkAlgNumWithIsolatingRectangle と mkAlgNumWithCComplex という名前で実装する。 前者は、既約多項式と分離領域(長方形)から AlgNum 型の値を作る。 後者は、既約とも無平方とも限らない多項式と、その根に収束する計算可能複素数(Complex CReal 型)から、 AlgNum 型の値を作る。 この辺は #12 で実装したものとほとんど同じである。 ただし、代数的数が実数である場合は、 FromReal データ構築子を使うように特別扱いする。
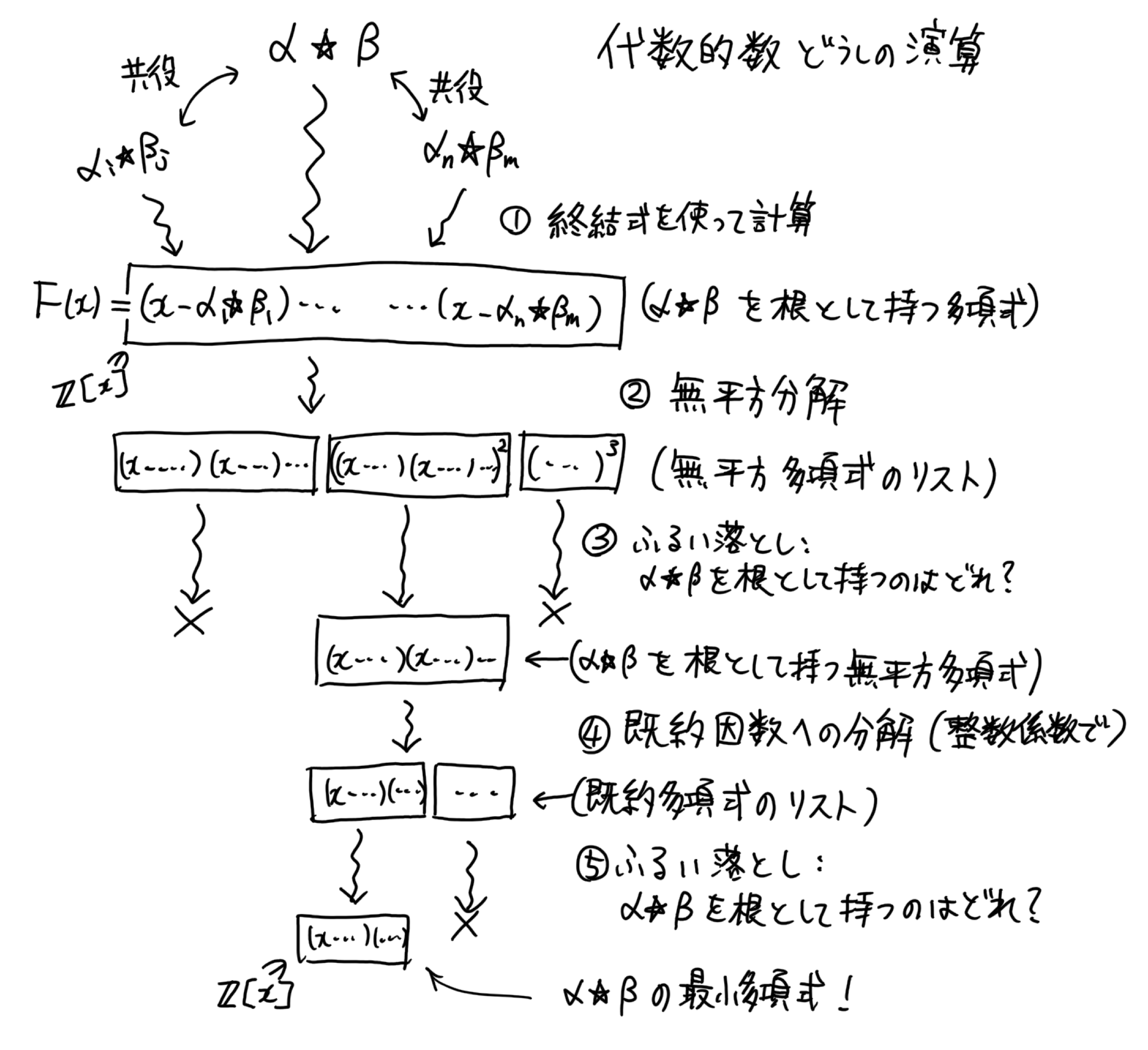
isCompatibleWithZeroR :: Complex Interval -> Bool
isCompatibleWithZeroR x = isCompatibleWithZero (realPart x) && isCompatibleWithZero (imagPart x)
compatibleRectangles :: Complex Interval -> Complex Interval -> Bool
compatibleRectangles x y = compatible (realPart x) (realPart y) && compatible (imagPart x) (imagPart y)
-- the polynomial: primitive, irreducible, leading coefficient > 0
mkAlgNumWithIsolatingRectangle :: UniPoly Integer -> Complex Interval -> AlgNum
mkAlgNumWithIsolatingRectangle f rect
| degree' f == 1 = fromRational $ - ((coeff f) V.! 0) % ((coeff f) V.! 1) -- rational number
| isCompatibleWithZero (imagPart rect)
, Iv a b <- realPart rect
, signAtZQ a f * signAtZQ b f < 0 = FromReal (mkAlgRealWithIrreduciblePoly f a b)
| otherwise = AlgNum f rect
mkAlgNumWithCComplex :: UniPoly Integer -> Complex CReal -> AlgNum
mkAlgNumWithCComplex f x = sieve squareFreeFactors (zipWith MkComplex (toIntervals $ realPart x) (toIntervals $ imagPart x))
where
squareFreeFactors :: [UniPoly Integer]
squareFreeFactors = map fst $ yun $ primitivePart f
sieve :: [UniPoly Integer] -> [Complex Interval] -> AlgNum
sieve [] _ = error "invalid complex number"
sieve [g] xs = sieve2 (unsafePerformIO (factorHenselIO g)) xs
sieve gs (x:xs) = sieve (filter (\g -> isCompatibleWithZeroR (valueAtZ x g)) gs) xs
sieve2 :: [UniPoly Integer] -> [Complex Interval] -> AlgNum
sieve2 [] _ = error "invalid complex number"
sieve2 [g] xs
| degree g <= Just 0 = error "mkAlgRealWithCComplex: minimal polynomial is constant"
| degree' g == 1 = fromRational $ - ((coeff g) V.! 0) % ((coeff g) V.! 1) -- rational number
| otherwise = case dropWhile (\r -> countRootsInRectangle g r True >= 2) xs of
r : _ -> mkAlgNumWithIsolatingRectangle g r
sieve2 gs (x:xs) = sieve2 (filter (\g -> isCompatibleWithZeroR (valueAtZ x g)) gs) xs代数的数を計算可能複素数としてみなすための関数 algNumToCComplex も実装する。 代数的実数の場合は二分法で区間の幅を半分ずつにしていったが、ここでは実部と虚部の幅をそれぞれ半分ずつ、つまり長方形を4分割している。
algNumToCComplex :: AlgNum -> Complex CReal
algNumToCComplex (FromReal x) = fromReal (algRealToCReal x)
algNumToCComplex x = let f = definingPolynomialN x
r0@(MkComplex r i) = isolatingRectangle x
rectangles = r0 : bisectReal r0
bisectReal rect = let Iv a b = realPart rect
leftHalf = MkComplex (Iv a ((a + b) / 2)) (imagPart rect)
rightHalf = MkComplex (Iv ((a + b) / 2) b) (imagPart rect)
in if countRootsInRectangle f leftHalf True == 0
then bisectImag rightHalf
else bisectImag leftHalf
bisectImag rect = let Iv c d = imagPart rect
lowerHalf = MkComplex (realPart rect) (Iv c ((c + d) / 2))
upperHalf = MkComplex (realPart rect) (Iv ((c + d) / 2) d)
in if countRootsInRectangle f lowerHalf True == 0
then upperHalf : bisectReal upperHalf
else lowerHalf : bisectReal lowerHalf
in MkComplex (CReal $ map realPart rectangles) (CReal $ map imagPart rectangles)代数的数の実部と虚部を返す関数と、実部と虚部から代数的数を作る関数を実装する:
-- 代数的数の実部を返す
realPartA :: AlgNum -> AlgReal
realPartA (FromReal x) = x
realPartA x = mkAlgRealWithCReal g (realPart (algNumToCComplex x))
where f = definingPolynomialN x
g = resultant_d (mapCoeff constP f) (compP (mapCoeff constP f) $ constP (scaleP 2 ind) - ind) -- res_y(f(y),f(2x-y))
-- 代数的数の虚部を返す
imagPartA :: AlgNum -> AlgReal
imagPartA (FromReal _) = 0
imagPartA x = mkAlgRealWithCReal h (imagPart (algNumToCComplex x))
where f = definingPolynomialN x
g = resultant_d (mapCoeff (constP . fromReal) f) (compP (mapCoeff (constP . fromReal) f) $ ind - constP (scaleP (fromImag 2) ind)) -- res_y(f(y),f(y-2ix))
h = gcdD (mapCoeff realPart g) (mapCoeff imagPart g)
-- 実部と虚部から代数的数を作る
mkComplexA :: AlgReal -> AlgReal -> AlgNum
mkComplexA x y = mkAlgNumWithCComplex h (MkComplex (algRealToCReal x) (algRealToCReal y))
where f = mapCoeff constP (definingPolynomial x)
g = mapCoeff (constP . constP) (definingPolynomial y)
h = resultant_d f $ resultant_d g $ (constP (constP ind - ind))^2 + ind^2 -- res_y(f(y),res_z(g(z),(x-y)^2+z^2))絶対値の2乗を計算する関数 squaredMagnitudeA, 絶対値を計算する関数 magnitudeA と、複素共役を計算する関数 complexConjugate を実装する:
rectangleToSquaredMagnitude :: Complex CReal -> CReal
rectangleToSquaredMagnitude z = (maxCReal 0 (realPart z))^2 + (maxCReal 0 (imagPart z))^2
-- 絶対値の2乗を計算する
squaredMagnitudeA :: AlgNum -> AlgReal
squaredMagnitudeA (FromReal x) = x * x
squaredMagnitudeA x = mkAlgRealWithCReal (resultant_poly y_f_x_y g) (rectangleToSquaredMagnitude $ algNumToCComplex x)
where f = definingPolynomialN x
y_f_x_y = UniPoly $ V.reverse $ V.imap (\i a -> constP a * ind^i) $ coeff f -- y^n f(x/y)
g = mapCoeff constP $ definingPolynomialN x
-- 代数的数の絶対値を計算する
magnitudeA :: AlgNum -> AlgReal
magnitudeA (FromReal x) = abs x
magnitudeA x = sqrtA (squaredMagnitudeA x)
-- 複素共役を計算する
complexConjugate :: AlgNum -> AlgNum
complexConjugate x@(FromReal _) = x
complexConjugate x = mkAlgNumWithIsolatingRectangle (definingPolynomialN x) (conjugate (isolatingRectangle x))Eq クラス、 Num クラスなどのインスタンスを実装する。 まあ、代数的実数の場合とだいたいパラレルだと思って良い。 実数と違い自然な全順序がないため、 Ord のインスタンスは実装しない。
abs と signum に関しては、筆者の個人的な立場としてはこれらは Num クラスに入っているべきではない。 しかし Data.Complex の Complex では
abs: 引数 z の絶対値を実部とし、虚部が 0 であるような複素数 \left\lvert z\right\rvert+0\sqrt{-1} を返すsignum: 引数が 0 の場合は 0, そうでない場合は引数を絶対値で割ったもの \frac{z}{\left\lvert z\right\rvert} を
と定義されており、これらは代数的数の場合でも問題なく定義できるため、ここでもそういう風に定義しておく。
instance Eq AlgNum where
FromReal x == FromReal y = x == y
x == y = definingPolynomialN x == definingPolynomialN y && compatibleRectangles (isolatingRectangle x) (isolatingRectangle y)
instance Num AlgNum where
negate (FromReal x) = FromReal (negate x)
negate x = mkAlgNumWithIsolatingRectangle (primitivePart $ compP (definingPolynomialN x) (-ind)) (- isolatingRectangle x)
FromReal x + FromReal y = FromReal (x + y)
x + y = mkAlgNumWithCComplex (resultant_poly f_x_y g) (algNumToCComplex x + algNumToCComplex y)
where f = mapCoeff constP $ definingPolynomialN x
f_x_y = compP f (constP ind - ind) -- f(x-y)
g = mapCoeff constP $ definingPolynomialN y
FromReal x * FromReal y = FromReal (x * y)
FromReal (FromRat k) * y
| k == 0 = 0
| otherwise = mkAlgNumWithIsolatingRectangle f_x_k (isolatingRectangle y * fromRational k)
where f_x_k = fst $ homogeneousValueAt (scaleP (denominator k) ind) (fromInteger $ numerator k) (mapCoeff fromInteger (definingPolynomialN y)) -- f(x/k)
x * y@(FromReal (FromRat _)) = y * x
x * y = mkAlgNumWithCComplex (resultant_poly y_f_x_y g) (algNumToCComplex x * algNumToCComplex y)
where f = definingPolynomialN x
y_f_x_y = UniPoly $ V.reverse $ V.imap (\i a -> constP a * ind^i) $ coeff f -- y^n f(x/y)
g = mapCoeff constP $ definingPolynomialN y
fromInteger n = FromReal (fromInteger n)
abs x = FromReal (magnitudeA x)
signum x | x == 0 = x
| otherwise = x / abs x
instance Fractional AlgNum where
recip (FromReal x) = FromReal (recip x)
recip x = mkAlgNumWithCComplex (UniPoly $ V.reverse $ coeff $ definingPolynomialN x) (recip (algNumToCComplex x))
fromRational x = FromReal (fromRational x)
instance IntegralDomain AlgNum where
divide = (/)
instance GCDDomain AlgNum where
gcdD = fieldGcd
contentV = fieldContentV平方根など
平方根 sqrtAN、n 乗根 nthRootAN、n乗 powIntAN、有理数乗 powRatAN、多項式への代入 valueAtAN も実装していく。 注意点としては、平方根および n 乗根の branch cut が負の虚軸(の第3象限側)となるようにする。
sqrtAN :: AlgNum -> AlgNum
sqrtAN (FromReal x)
| x >= 0 = FromReal (sqrtA x)
| otherwise = mkComplexA 0 (sqrtA (-x))
sqrtAN x = nthRootAN 2 x
nthRootAN :: Int -> AlgNum -> AlgNum
nthRootAN n (FromReal x)
| x >= 0 || odd n = FromReal (nthRootA n x)
| otherwise = mkComplexA 0 (nthRootA n (-x))
nthRootAN n x
| n == 0 = error "0th root"
| n < 0 = nthRootAN (-n) (recip x)
| x == 0 = 0
| otherwise = sieve (map (\(y,_) -> (y,algNumToCComplex y)) $ rootsI (compP f (ind^n)))
where f = definingPolynomialN x
sieve :: [(AlgNum,Complex CReal)] -> AlgNum
sieve [] = error "nthRootAN"
sieve [(y,_)] = y
sieve ys = sieve $ map (\(y,cz) -> (y,fmap (CReal . tail . toIntervals) cz)) $ filter (\(y,cz) -> isCompatible (fmap (head . toIntervals) cz)) ys
isCompatible :: Complex Interval -> Bool
isCompatible z = compatibleRectangles (isolatingRectangle x) (z^n) && if isImagPartPositive then b >= 0 else a <= 0
where Iv a b = imagPart z
-- x is assumed to be non-real
isImagPartPositive = unsafeCompareCReal 0 (imagPart (algNumToCComplex x)) == LT
powIntAN :: AlgNum -> Int -> AlgNum
powIntAN _ 0 = 1
powIntAN (FromReal x) n = FromReal (powIntA x n)
powIntAN x n | n < 0 = recip $ powIntAN x (-n)
powIntAN x n = case (ind^n) `modP` f of
g -> valueAt x (mapCoeff fromRational g) -- x^n mod f(x) (ind^n `modP` f)
where f = mapCoeff fromInteger $ definingPolynomialN x :: UniPoly Rational
powRatAN :: AlgNum -> Rational -> AlgNum
powRatAN x y = powIntAN (nthRootAN (fromInteger $ denominator y) x) (fromInteger $ numerator y)
valueAtAN :: AlgNum -> UniPoly Rational -> AlgNum
valueAtAN (FromReal x) f = FromReal (valueAtA x f)
valueAtAN x f = case f `modP` g of
h -> valueAt x (mapCoeff fromRational h)
where g = mapCoeff fromInteger $ definingPolynomialN x :: UniPoly Rational多項式の根
多項式の根を列挙する操作を実装しよう。
まず、「既約な整数係数多項式の、指定した長方形内の根を全て列挙する」という操作を実装する。 実部と虚部にそれぞれ二分法を適用し、ふるい分けていく。 長方形内の根の個数がただ1つとなった場合は、それが分離長方形となるので、それを返す。 この二分法を適用する際、「長方形の右と上の辺は含むが、左と下の辺は含まない」としておくと便利である。
rootsOfIrreduciblePolyInRectangle :: UniPoly Integer -> Complex Interval -> Int -> [AlgNum]
rootsOfIrreduciblePolyInRectangle f rect expectedNumOfRoots = bisectReal rect expectedNumOfRoots
where
bisectReal rect n
| n == 0 = []
| n == 1 && countRootsInRectangle f rect True == 1 = [mkAlgNumWithIsolatingRectangle f rect]
| otherwise = let Iv a b = realPart rect
leftHalf = MkComplex (Iv a ((a + b) / 2)) (imagPart rect)
rightHalf = MkComplex (Iv ((a + b) / 2) b) (imagPart rect)
m = countRootsInRectangle f leftHalf False
in if m == 0
then bisectImag rightHalf n
else if m == n
then bisectImag leftHalf n
else bisectImag leftHalf m ++ bisectImag rightHalf (n - m)
bisectImag rect n
| n == 0 = []
| n == 1 && countRootsInRectangle f rect True == 1 = [mkAlgNumWithIsolatingRectangle f rect]
| otherwise = let Iv c d = imagPart rect
lowerHalf = MkComplex (realPart rect) (Iv c ((c + d) / 2))
upperHalf = MkComplex (realPart rect) (Iv ((c + d) / 2) d)
m = countRootsInRectangle f lowerHalf False
in if m == 0
then bisectReal upperHalf n
else if m == n
then bisectReal lowerHalf n
else bisectReal lowerHalf m ++ bisectReal upperHalf (n - m)整数係数、有理数係数多項式の根を全て列挙する関数をそれぞれ rootsI, rootsQ という名前で実装する。
rootsI :: UniPoly Integer -> [(AlgNum,Int)]
rootsI f | f == 0 = error "rootsI: zero"
| otherwise = [ (x,i)
| (g,i) <- yun (primitivePart f)
, h <- sortPolynomials $ unsafePerformIO (factorHenselIO g)
, let bound = rootBound h
, x <- rootsOfIrreduciblePolyInRectangle h (MkComplex (Iv (-bound) bound) (Iv (-bound) bound)) (degree' h)
]
where sortPolynomials :: [UniPoly Integer] -> [UniPoly Integer]
sortPolynomials = sortOn coeff
rootsQ :: UniPoly Rational -> [(AlgNum,Int)]
rootsQ f = let commonDenominator = V.foldl' (\a b -> lcm a (denominator b)) 1 (coeff f)
fz = primitivePart $ mapCoeff (\x -> numerator x * (commonDenominator `div` denominator x)) f
in rootsI fz次に、代数的実数係数多項式の根を全て列挙する操作を rootsA という名前で実装する。 終結式を使って整数係数に直す操作は前回実装した elimN を使える。
rootsA :: UniPoly AlgReal -> [(AlgNum,Int)]
rootsA f = [ (x,i)
| (g,i) <- yun f
, (x,_) <- rootsI (elimN g)
, let rect = isolatingRectangle x
, countRootsInRectangleAN (mapCoeff FromReal f) rect True > 0
]さて、「整数係数多項式の根が指定された領域にいくつあるか」を計算する操作は実装したが、「代数的数を係数とする多項式の根が指定された領域にいくつあるか」を計算する操作はまだ実装していない。 非常に残念なことだが、ほとんど同じコードをもう一度書くことになる。 型クラス等を使ってコードを一本化したいところだが、今後の課題としたい。
negativePRSOnPathAN :: UniPoly AlgNum -> UniPoly (Complex Integer) -> Complex Integer -> ([UniPoly AlgReal], UniPoly AlgReal)
negativePRSOnPathAN f c d = (s, uv)
where
fc = fst $ homogeneousCompP f (mapCoeff complexIntToAlgNum c) (complexIntToAlgNum d)
u = mapCoeff realPartA fc
v = mapCoeff imagPartA fc
uv = gcdD u v
u' = u `divide` uv
v' = v `divide` uv
s | degree u' > degree v' = negativePRS u' v'
| otherwise = u' : negativePRS v' (-u')
complexIntToAlgNum :: Complex Integer -> AlgNum
complexIntToAlgNum z = mkComplexA (fromInteger $ realPart z) (fromInteger $ imagPart z)
complexRatToAlgNum :: Complex Rational -> AlgNum
complexRatToAlgNum z = mkComplexA (fromRational $ realPart z) (fromRational $ imagPart z)
-- c(t) = t + k * sqrt (-1)
negativePRSOnHorizontalLineAN :: UniPoly AlgNum -> Rational -> ([UniPoly AlgReal], UniPoly AlgReal)
negativePRSOnHorizontalLineAN f k = negativePRSOnPathAN f (scaleP (fromReal q) ind + constP (fromImag p)) (fromReal q)
where p = numerator k
q = denominator k
-- c(t) = k + t * sqrt (-1)
negativePRSOnVerticalLineAN :: UniPoly AlgNum -> Rational -> ([UniPoly AlgReal], UniPoly AlgReal)
negativePRSOnVerticalLineAN f k = negativePRSOnPathAN f (constP (fromReal p) + scaleP (fromImag q) ind) (fromReal q)
where p = numerator k
q = denominator k
countRootsInRectangleAN :: UniPoly AlgNum -> Complex Interval -> Bool -> Int
countRootsInRectangleAN f rect includeLeftAndBottomEdges
| a == b && c == d = if atTopLeft then 1 else 0
| a == b = onRightEdge + (if atTopRight then 1 else 0) + (if atBottomRight then 1 else 0)
| c == d = onTopEdge + (if atTopLeft then 1 else 0) + (if atTopRight then 1 else 0)
| otherwise = (totalVariation `div` 2) + corners
where
Iv a b = realPart rect
Iv c d = imagPart rect
-- corners
-- 4隅に根をもたないようにする
bottomLeft = MkComplex a c
bottomRight = MkComplex b c
topLeft = MkComplex a d
topRight = MkComplex b d
atBottomLeft = valueAt (complexRatToAlgNum bottomLeft) f == 0
atBottomRight = valueAt (complexRatToAlgNum bottomRight) f == 0
atTopLeft = valueAt (complexRatToAlgNum topLeft) f == 0
atTopRight = valueAt (complexRatToAlgNum topRight) f == 0
cornerFactors = mapCoeff complexRatToAlgNum $ product [ if atBottomLeft then ind - constP bottomLeft else 1
, if atBottomRight then ind - constP bottomRight else 1
, if atTopLeft then ind - constP topLeft else 1
, if atTopRight then ind - constP topRight else 1
]
-- 4隅にある根の数
corners = length $ filter id [ includeLeftAndBottomEdges && atBottomLeft
, includeLeftAndBottomEdges && atBottomRight
, includeLeftAndBottomEdges && atTopLeft
, atTopRight
]
fr :: UniPoly AlgNum -- f から、長方形の4隅の根を取り除いたもの
fr = f `divide` cornerFactors
g1, g2, g3, g4 :: UniPoly AlgReal
s1, s2, s3, s4 :: [UniPoly AlgReal]
(s1,g1) = negativePRSOnHorizontalLineAN fr c
(s2,g2) = negativePRSOnVerticalLineAN fr b
(s3,g3) = negativePRSOnHorizontalLineAN fr d
(s4,g4) = negativePRSOnVerticalLineAN fr a
onBottomEdge = countRealRootsBetween (fromRational a) (fromRational b) g1
onRightEdge = countRealRootsBetween (fromRational c) (fromRational d) g2
onTopEdge = countRealRootsBetween (fromRational a) (fromRational b) g3
onLeftEdge = countRealRootsBetween (fromRational c) (fromRational d) g4
varOnBottomEdge = varianceAt (fromRational b) s1 - varianceAt (fromRational a) s1
varOnRightEdge = varianceAt (fromRational d) s2 - varianceAt (fromRational c) s2
varOnTopEdge = varianceAt (fromRational a) s3 - varianceAt (fromRational b) s3
varOnLeftEdge = varianceAt (fromRational c) s4 - varianceAt (fromRational d) s4
rootsOnEdges = onRightEdge + onTopEdge - negateIf includeLeftAndBottomEdges (onBottomEdge + onLeftEdge)
totalVariation = varOnBottomEdge + varOnRightEdge + varOnTopEdge + varOnLeftEdge + rootsOnEdges最後に、「代数的数係数の多項式の根を全て列挙する」操作 rootsAN を実装する。
toMultPolyAN :: (Eq a, Num a) => UniPoly a -> MultPoly (UniPoly Integer)
toMultPolyAN 0 = 0
toMultPolyAN f = sum [multInd i * Scalar (ind^i) | i <- [0..degree' f]]
-- Eliminate algebraic numbers in the coefficients by multiplying conjugates
elimNN :: UniPoly AlgNum -> UniPoly Integer
elimNN f = case loop (toMultPolyAN f) polynomialsForCoefficients of
Just g -> g
Nothing -> error "elimNN: internal error"
where
polynomialsForCoefficients = V.map definingPolynomialN (coeff f)
loop :: MultPoly (UniPoly Integer) -> V.Vector (UniPoly Integer) -> Maybe (UniPoly Integer)
loop m v | V.null v = multToScalar m
loop m v = loop (resultant_d (mapCoeff (Scalar . constP) (V.head v)) (multToUni m)) (V.tail v)
rootsAN :: UniPoly AlgNum -> [(AlgNum,Int)]
rootsAN f = [ (x,i)
| (g,i) <- yun f
, (x,_) <- rootsI (elimNN g)
, let rect = isolatingRectangle x
, countRootsInRectangleAN f rect True > 0
]これで、代数閉体としての操作が一通り実装できた。
他のモジュール
早速 REPL で試したいところだが、既存のモジュールにもいくつか手を加える必要がある。 まず、 AlgReal.hs の mkAlgRealWithIrreduciblePoly 関数について、最初の条件チェックが b <= a になっているのを b < a に直す:
-- AlgReal.hs
mkAlgRealWithIrreduciblePoly :: UniPoly Integer -> Rational -> Rational -> AlgReal
mkAlgRealWithIrreduciblePoly f a b
-- 区間が空の場合はエラー
| b < a = error "mkAlgReal: empty range"
-- ...略【2018年3月6日 追加】 isolatingInterval' 関数を次のように定義する:
isolatingInterval' :: AlgReal -> Interval
isolatingInterval' (FromRat x) = Iv x x
isolatingInterval' (AlgReal _ _ x y) = Iv x yCReal.hs にいくつか関数を追加する:
-- CReal.hs に追加
toIntervals :: CReal -> [Interval]
toIntervals (CReal xs) = xs
maxCReal :: CReal -> CReal -> CReal
maxCReal (CReal xs) (CReal ys) = CReal (zipWith maxInterval xs ys)
minCReal :: CReal -> CReal -> CReal
minCReal (CReal xs) (CReal ys) = CReal (zipWith minInterval xs ys)Interval.hs にもいくつか関数を追加する:
-- Interval.hs に追加
maxInterval :: Interval -> Interval -> Interval
maxInterval (Iv a b) (Iv a' b') = Iv (max a a') (max b b')
minInterval :: Interval -> Interval -> Interval
minInterval (Iv a b) (Iv a' b') = Iv (min a a') (min b b')
compatible :: Interval -> Interval -> Bool
compatible (Iv a b) (Iv a' b') = a <= b' && a' <= b【2018年3月6日 更新】 compatible 関数が抜けていたので追加した。
そして、 Haskell 経験のある諸君は気づいているかもしれないが、今回書いたコードで使っている Complex 型というのは Data.Complex のそれではない。 Data.Complex は浮動小数点数しか考慮しておらず、整数、有理数、区間演算、計算可能実数などに対して適用できない。 そのため、自前で、汎用的な複素数型を実装する。
src/Numeric/AlgebraicReal/Complex.hs に以下を書く:
{-# LANGUAGE DeriveFunctor #-}
module Numeric.AlgebraicReal.Complex where
import Numeric.AlgebraicReal.Class
data Complex a = MkComplex !a !a
deriving (Eq,Show,Functor)
fromReal :: (Num a) => a -> Complex a
fromReal x = MkComplex x 0
fromImag :: (Num a) => a -> Complex a
fromImag y = MkComplex 0 y
realPart, imagPart :: Complex a -> a
realPart (MkComplex x _) = x
imagPart (MkComplex _ y) = y
conjugate :: (Num a) => Complex a -> Complex a
conjugate (MkComplex x y) = MkComplex x (- y)
instance (Num a) => Num (Complex a) where
-- 'RealFrac a' is not required!
negate (MkComplex x y) = MkComplex (negate x) (negate y)
MkComplex x y + MkComplex x' y' = MkComplex (x + x') (y + y')
MkComplex x y - MkComplex x' y' = MkComplex (x - x') (y - y')
MkComplex x y * MkComplex x' y' = MkComplex (x * x' - y * y') (x * y' + y * x')
fromInteger n = MkComplex (fromInteger n) 0
abs = undefined
signum = undefined
instance (Fractional a) => Fractional (Complex a) where
recip (MkComplex x y) = let r = recip (x^2 + y^2)
in MkComplex (x * r) (negate y * r)
fromRational x = MkComplex (fromRational x) 0
instance (IntegralDomain a) => IntegralDomain (Complex a) where
divide (MkComplex x y) (MkComplex x' y') = let d = x'^2 + y'^2
in MkComplex ((x * x' + y * y') `divide` d) ((y * x' - x * y') `divide` d)試す
いつものように stack repl を実行する。
\sqrt{-1} を計算してみよう。
> sqrtAN (-1)
AlgNum (UniPoly [1,0,1]) (MkComplex (Iv (0 % 1) (0 % 1)) (Iv (1 % 1) (1 % 1)))
> let i = it
> i^2
FromReal (FromRat ((-1) % 1))
> (1+i)^2
AlgNum (UniPoly [4,0,1]) (MkComplex (Iv (0 % 1) (0 % 1)) (Iv (2 % 1) (2 % 1)))
> realPartA ((1+i)^2)
FromRat (0 % 1)
> imagPartA ((1+i)^2)
FromRat (2 % 1)
> (1+i)^4
FromReal (FromRat ((-1) % 4))表示の仕方(Show インスタンスの実装)に工夫の余地があるが、それっぽい計算ができている。
1の3乗根を計算してみよう。
> rootsI (ind^3-1)
[(FromReal (FromRat (1 % 1)),1),(AlgNum (UniPoly [1,1,1]) (MkComplex (Iv ((-2) % 1) (0 % 1)) (Iv ((-2) % 1) (0 % 1))),1),(AlgNum (UniPoly [1,1,1]) (MkComplex (Iv ((-2) % 1) (0 % 1)) (Iv (0 % 1) (2 % 1))),1)]
> let [a0,a1,a2] = map fst it
> realPartA a1
FromRat ((-1) % 2)
> imagPartA a1
AlgReal (UniPoly [-3,0,4]) (-1) ((-1) % 1) ((-3) % 4)
> (imagPartA a1)^2
FromRat (3 % 4)
> imagPartA a1 < 0
True実部が -\frac{1}{2}、虚部の2乗が \frac{3}{4} で符号が負であることから、1の3乗根の1つが \frac{-1-\sqrt{-3}}{2} であることが計算できたことになる。
\sqrt{i} を計算してみよう。
> sqrtAN i
AlgNum (UniPoly [1,0,0,0,1]) (MkComplex (Iv (0 % 1) (2 % 1)) (Iv (0 % 1) (2 % 1)))
> realPartA (sqrtAN i)
AlgReal (UniPoly [-1,0,2]) 1 (5 % 8) (3 % 4)
> it^2
FromRat (1 % 2)
> imagPartA (sqrtAN i)
AlgReal (UniPoly [-1,0,2]) 1 (5 % 8) (3 % 4)
> it^2
FromRat (1 % 2)\sqrt{i} が \frac{1}{\sqrt{2}}+\frac{i}{\sqrt{2}} と計算できている。
代数的数を係数とする多項式の根も求めてみよう。 まずは1次の場合 x-\sqrt{-1} から。
> rootsAN (ind - constP i)
[(AlgNum (UniPoly [1,0,1]) (MkComplex (Iv ((-2) % 1) (0 % 1)) (Iv (0 % 1) (2 % 1))),1)]まあ、1次の場合は簡単だろう。
2次の場合。
> rootsAN (ind^2 - constP i)…筆者の環境では ghci がメモリが食いつぶし、強制終了する羽目になった。
どうやら、代数的数を係数とする多項式の虚根の数え上げで、とてつもないコストがかかっているように思える。 真面目に工夫すればもうちょっと実用的になるだろうが、筆者の気力が尽きようとしているので、ここまでにしておく。
【2018年3月6日 更新】 AlgNum に対する * の定義がバグっていたので修正した。
> rootsAN (ind^2 - constP i)
[(AlgNum (UniPoly [1,0,0,0,1]) (MkComplex (Iv ((-2) % 1) (0 % 1)) (Iv ((-2) % 1) (0 % 1))),1),(AlgNum (UniPoly [1,0,0,0,1]) (MkComplex (Iv (0 % 1) (2 % 1)) (Iv (0 % 1) (2 % 1))),1)]TODO: 書く
最後に
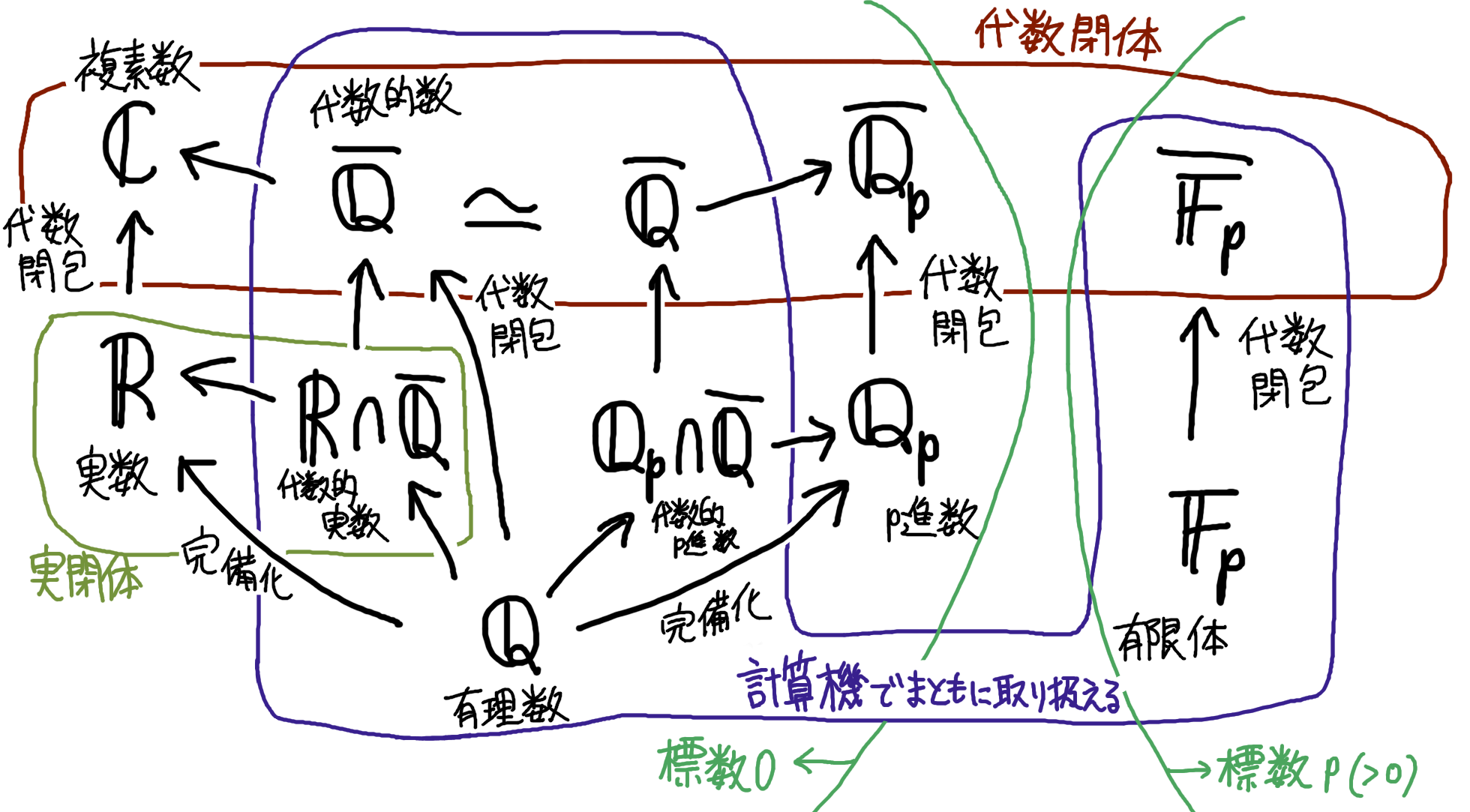
連載開始から16回、4ヵ月半の時間をかけて、我々はようやく「計算機で(等号も含めて)扱える代数閉体」を実装することができた(ということにする)。 この応用は色々考えられる。
- 代数的実数係数の多項式を、1次または2次の因数に、既約分解できる。
- 有理関数を部分分数分解し、不定積分の計算ができる。
- 行列の固有値を正確に取り扱える。
- 実閉体の量化子除去(または限量子除去; quantifier elimination, QE)を実装するという方向性もありそうだ。
- 超越拡大 \overline{\mathbf{Q}}(\pi) によって、「\pi を正確に取り扱いたい」という需要に部分的に応えられるかもしれない。ただし、四則演算は可能だが、平方根などの演算は自由にはできなくなる。
- 作図可能な数は代数的数(の部分体)なので、初等幾何の作図を浮動小数点数の誤差に煩わされずに正確に行えそうだ。
あるいは、他の数学的対象を実装するという方向性もある:
- p 進数:今回の実装では、根を分離(区別)するのに、区間や領域、つまり実数 \mathbf{R} ・複素数 \mathbf{C} の位相構造を利用している。これとは別の方向性で、 p 進数 \mathbf{Q}_p の位相構造に基づいた分離もできるのではないだろうか。代数的 p 進数 \mathbf{Q}_p\cap\overline{\mathbf{Q}} を実装してみるのも一興かもしれない。
- 有限体の代数閉包 \overline{\mathbf{F}_p} も実装できそうではある。標数 0 の場合は、複素数への埋め込み \overline{\mathbf{Q}}\subset\mathbf{C} によって根を分離できたが、有限体の場合はそういう「頼れる埋め込み先」が思い当たらない。
- 代数的整数とは、最小多項式が整数係数モニック多項式として書けるような代数的数である。代数的整数の演算について掘り下げるということも考えられる。
愚直に、実装のさらなる改良に励むという手もある(真面目に応用するなら、これらは避けて通れないだろう):
- 終結式の計算の改良:簡単なプロファイリングによると、終結式の計算に時間がかかっている。そのため、終結式の計算方法を改良したい。
- 多変数多項式の表し方の改良:現在は2変数多項式を素朴に
UniPoly (UniPoly a)という形で表しているが、もっと効率的な表し方を実装したい。 - 多項式の因数分解アルゴリズムの改良:多項式の因数分解は、モジュラー因数を組み合わせる際に総当たりを行なっている。そのため、最悪計算量は指数オーダーとなる。そこを改良したい。
- 根号を使った表示:現在は、代数的数を印字した際に、(有理数じゃない場合は)最小多項式と区間を使って表示している。しかし、一部の代数的数は根号を使って表示できるはずで、そういう数は根号を使って表示した方が見やすいのではないか。というわけで、代数的数を根号で表すアルゴリズムがあるのか、調査してみると良いかもしれない。
- 代数的数の表し方の変更:現在は、ひとつの代数的数を、ひとつの多項式(最小多項式)で表している。すると、四則演算のたびに最小多項式を計算し直す羽目になる。ここに改良の余地があるのではないか。
どれも面白そうなトピックであるが、これまでのような「週刊」というペースでやっていくには筆者の予備知識が足りないし、何より筆者の身がもたない。 そのため、今後は不定期的に更新することになるだろう。