#14 代数的実数を係数とする代数方程式
#2 実根の数え上げ では「整数係数または有理数係数の方程式の根」を求める操作を実装したが、「代数的実数を係数とする方程式の根」を求める操作はまだ実装していない。 今回はこれを実装する。
代数的実数を係数とする代数方程式
代数的実数を係数とする代数方程式を解きたい。 つまり、 a_nx^n+\cdots+a_1x+a_0=0 の a_i が代数的実数の場合に、その実根を計算したい。
代数的実数の定義は「有理数係数多項式の根となる実数」だったが、代数的実数を係数とする多項式の実根も再び代数的実数となる。
#3 代数的数の演算と終結式 で代数的数の演算を実装した際、登場する代数的数の共役も含めて考えることで、代数的数を消去して有理数のみの多項式を得ることができた。 その際、終結式を使うと代数的数を消去できるのだった。
今回も同じように、係数として登場する代数的数の共役も含めて考えることによって、係数の代数的数を消去することにする。 係数として複数の代数的数が登場しうるので、終結式を繰り返し使うことになる。
代数的数を係数とする多項式 f から代数的数を消去した後の有理数係数多項式 F は、もとの多項式よりも次数が上がるので、根が水増しされている可能性がある。 従って、 F の根を列挙した後に、それがもとの多項式 f の根であるかどうかチェックする必要がある。
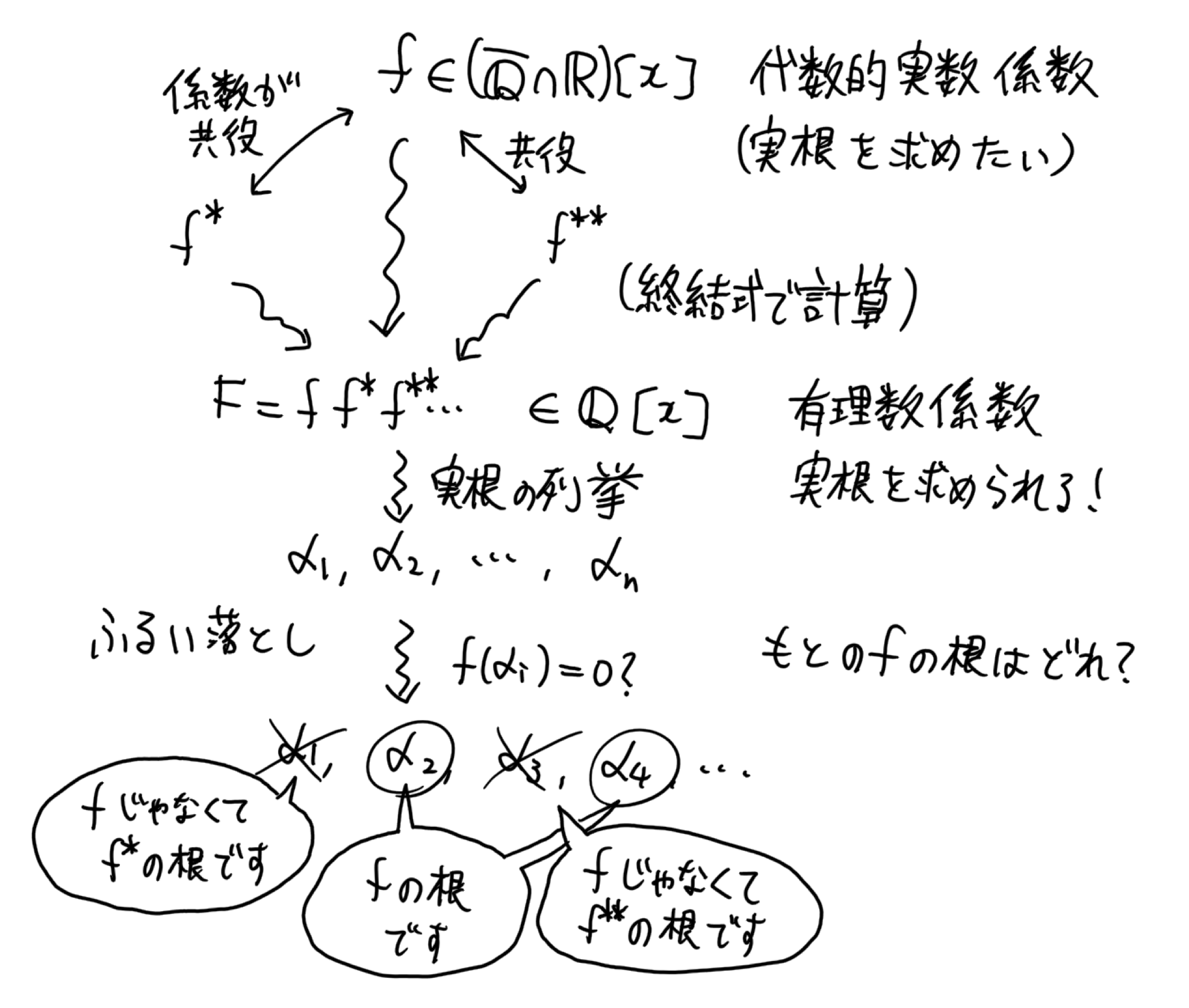
例1 2次の多項式 f(x)=x^2-x-(1+\sqrt{2}) の実根を計算しよう。 この多項式の係数に登場する(真の)代数的数は 1+\sqrt{2} で、その共役は 1-\sqrt{2} である。 よって、係数の共役をとった多項式 f^*(x)=x^2-x-(1-\sqrt{2}) も考えて、 f と f^* の積をとる: \begin{aligned} F(x)=f(x)f^*(x) &=(x^2-x-(1+\sqrt{2}))(x^2-x-(1-\sqrt{2})) \\ &=x^4-2x^3-x^2+2x-1 \end{aligned} 無事に係数から根号が消え、有理数係数の多項式 F が得られた。 この多項式 F は2個の実根 -\frac{3}{2}<\alpha_1<-\frac{3}{4}, \frac{3}{2}<\alpha_2<3 を持つ。 \alpha_1, \alpha_2 はそれぞれ f または f^* の根である。 そこで f(\alpha_1), f(\alpha_2) をそれぞれ計算してやると、 f(\alpha_1)=f(\alpha_2)=0 となり、 \alpha_1, \alpha_2 の両方とも f の根であることがわかる。 よって、 f の根は \alpha_1 と \alpha_2 の2つである。

例2 2次の多項式 f(x)=x^2-(1+\sqrt{2})x-\sqrt{3} の実根を計算しよう。 係数の共役をとった式は \begin{gathered} x^2-(1+\sqrt{2})x-\sqrt{3}, \\ x^2-(1-\sqrt{2})x-\sqrt{3}, \\ x^2-(1+\sqrt{2})x+\sqrt{3}, \\ x^2-(1-\sqrt{2})x+\sqrt{3} \end{gathered} の4つなので、それらの積をとる: \begin{gathered} F(x)= (x^2-(1+\sqrt{2})x-\sqrt{3}) (x^2-(1-\sqrt{2})x-\sqrt{3}) (x^2-(1+\sqrt{2})x+\sqrt{3}) (x^2-(1-\sqrt{2})x+\sqrt{3}) \\ =x^8-4x^7+2x^6+4x^5-5x^4+12x^3-18x^2+9 \end{gathered} すると、 \sqrt{2} や \sqrt{3} が消去された、有理数係数の多項式が得られた。 この有理数係数多項式 F(x)=x^8-4x^7+2x^6+4x^5-5x^4+12x^3-18x^2+9 の根を列挙すると、4個の根 \alpha_1<\alpha_2<\alpha_3<\alpha_4 があることがわかる(前回の例として取り上げたのはこの多項式である)。 あとは、それらのうち、実際にもとの方程式の根となるのはどれなのか、代入して確かめてやれば良い。 f(\alpha_1)=?,\quad f(\alpha_2)=?,\quad f(\alpha_3)=?,\quad f(\alpha_4)=? …なのだが、前回の例で見たように、これを直接代数的実数として計算するのはとてつもないコストがかかる。 そこで、この部分の高速化を後で考えることにする。 (先に答えを書いておくと、 f(\alpha_1)\ne 0,\quad f(\alpha_2)=0,\quad f(\alpha_3)\ne 0,\quad f(\alpha_4)=0 となり、 \alpha_2 と \alpha_4 が f の根である。)

終結式の利用
根を求めたい多項式 f(x)=a_nx^n+\cdots+a_1x+a_0 に対して、係数を変数に置き換えたものを \tilde{f}(y_0,y_1,\ldots,y_n,x)=y_nx^n+\cdots+y_1x+y_0 とおく。 代数的数 a_i の最小多項式(整数係数)を g_i(y_i)=b_i(y_i-a_i^{(1)})\cdots (y_i-a_i^{(m_i)}) とおき、 g_i の根(a_i の共役)を a_i^{(1)},\ldots,a_i^{(m_i)} とおく。 すると、代数的数を消去した後の多項式 F は F(x)=\prod_{j_0=1}^{m_0} \prod_{j_1=1}^{m_1} \cdots \prod_{j_n=1}^{m_n} \tilde{f}(a_0^{(j_0)},\ldots,a_n^{(j_n)},x) と書ける。 この F を、 g_i たちの係数(終結式)を使って表したい。
まず、変数 y_0 について終結式と根の関係を適用しよう。 F(x)\sim\operatorname{res}_{y_0}\biggl(g_0(y_0),\prod_{j_1=1}^{m_1} \cdots \prod_{j_n=1}^{m_n} \tilde{f}(y_0,a_1^{(j_1)}\ldots,a_n^{(j_n)},x)\biggr) ただし、 F の計算において定数倍は関係ないので、定数倍を無視するという意味で = の代わりにここでは \sim と書いている。
同様に、変数 y_1 について終結式と根の関係を適用できる。 F(x)\sim\operatorname{res}_{y_0}\biggl(g_0(y_0),\operatorname{res}_{y_1}\biggl(g_1(y_1),\prod_{j_2=1}^{m_2} \cdots \prod_{j_n=1}^{m_n} \tilde{f}(y_0,y_1,a_2^{(j_2)}\ldots,a_n^{(j_n)},x)\biggr)\biggr)
この操作を繰り返していけば、代数的数 a_i^{(j_i)} を F から完全に消去できる: F(x)\sim\operatorname{res}_{y_0}\bigl(g_0(y_0),\operatorname{res}_{y_1}\bigl(g_1(y_1),\cdots\operatorname{res}_{y_n}\bigl(g_n(y_n),\tilde{f}(y_0,y_1,\ldots,y_n,x)\bigr)\cdots\bigr)\bigr)\in\mathbb{Z}[x]
多変数多項式の実装
終結式を繰り返し使うためには、多変数多項式 R[x_1,x_2,\ldots,x_n] が必要である。
知っての通り、多変数多項式は、一変数多項式の組み合わせで書ける: R[x_1,x_2,\ldots,x_n]=R[x_1][x_2]\cdots[x_n] これまでは変数の個数が決まっていたため、 R[x,y]=R[x][y] を UniPoly (UniPoly a) というような型で表現できた。 しかし、今回の用途では変数の個数は動的に決まるため、 UniPoly を素朴に組み合わせることはできない。
そこで、多変数多項式環に対応する型を専用に用意する。 多変数多項式環の実装を1から書くのは面倒なので、可算無限個の変数を持つ多項式の型を「一変数多項式環を無限回重ねたもの」として実装し、基本的な演算については一変数多項式環の実装を流用できるようにする。 やる気があれば、もっと効率の良い表し方を採用するべきだろう。
具体的には、 k 変数多項式環 R_k を次のように定義し、 R_0=R,\quad R_k=R[x_{k-1}]\cdots[x_0][x_0] それらの和を R_\infty:=\bigcup_{k=0}^\infty R_k とおく。 R_\infty が、今回作る「可算無限個の変数を持つ多項式環」である。
変数の添字を付け替えて R_{k-1} を R_k に埋め込む写像 \mathrm{shift}\colon R[x_{k-2}]\cdots[x_0]\to R[x_{k-1}]\cdots[x_1]\subset R_k と書くことにすると、 \begin{gathered} R_k=\mathrm{shift}(R_{k-1})[x_0],\\ R_\infty=\mathrm{shift}(R_\infty)[x_0] \end{gathered} が成り立つ。
実装は src/Numeric/AlgebraicReal/MultPoly.hs に書く:
module Numeric.AlgebraicReal.MultPoly where
import Numeric.AlgebraicReal.Class
import Numeric.AlgebraicReal.UniPoly
-- multivariate polynomial
data MultPoly a = Poly !(UniPoly (MultPoly a))
| Scalar !a
deriving (Show)MultPoly a が R_\infty に相当するデータ型である。 Poly は \mathrm{shift} に相当するデータ構築子であり、 Scalar は係数環 R を R_\infty に埋め込むデータ構築子である。
この表現を使うと、 k 番目の不定元 x_k は次のようにして得られる:
-- R[multInd n][multInd (n-1)] ... [multInd 1][multInd 0]
multInd :: (Eq a, Num a) => Int -> MultPoly a
multInd 0 = Poly ind
multInd n | n > 0 = Poly $ constP $ multInd (n - 1)R_\infty を x_0 についての一変数多項式環 \mathrm{shift}(R_\infty)[x_0] としてみなす関数 multToUni は次のように書ける:
multToUni :: (Eq a, Num a) => MultPoly a -> UniPoly (MultPoly a)
multToUni (Poly f) = f
multToUni (Scalar k) = constP (Scalar k)R_\infty の元が定数であることが分かっている場合に、係数環の元として取り出す関数 multToScalar は次のように書ける:
multToScalar :: (Eq a, Num a) => MultPoly a -> Maybe a
multToScalar (Poly _) = Nothing
multToScalar (Scalar k) = Just k本当は Poly の場合にも定数かどうか確かめた方が良いのだろうが、今回の用途では必要ない。
等号の判定は次のように書ける:
instance (Eq a, Num a) => Eq (MultPoly a) where
Poly f == Poly g = f == g
Scalar k == Scalar l = k == l
f == g = multToUni f == multToUni g環演算は次のように書ける:
instance (Eq a, Num a) => Num (MultPoly a) where
negate (Poly x) = Poly (negate x)
negate (Scalar x) = Scalar (negate x)
Scalar x + Scalar y = Scalar (x + y)
f + g = Poly (multToUni f + multToUni g)
Scalar x * Scalar y = Scalar (x * y)
Poly x * Poly y = Poly (x * y)
Poly x * k@(Scalar _) = Poly (scaleP k x)
k@(Scalar _) * Poly y = Poly (scaleP k y)
fromInteger k = Scalar (fromInteger k)
abs = undefined
signum = undefined整域としての演算も書ける:
instance (Eq a, IntegralDomain a) => IntegralDomain (MultPoly a) where
divide (Scalar x) (Scalar y) = Scalar (divide x y)
divide (Poly f) (Poly g) = Poly (divide f g)
divide (Poly f) k@(Scalar _) = Poly (unscaleP k f)
divide k@(Scalar _) (Poly g) = Poly (divide (constP k) g)
instance (Eq a, GCDDomain a) => GCDDomain (MultPoly a) where
gcdD (Scalar f) (Scalar g) = Scalar (gcdD f g)
gcdD f g = Poly (gcdD (multToUni f) (multToUni g))いずれも、 multToUni 関数を使って UniPoly の演算に帰着させているだけである。
書き終わったら、 algebraic-real.cabal の exposed-modules: に追加しておこう。
exposed-modules: Numeric.AlgebraicReal.UniPoly
, ...
, Numeric.AlgebraicReal.MultPoly根の計算: Haskell での実装
多変数多項式の実装を用意できたので、本題である「代数的実数を根とする多項式の根を求める操作」を実装しよう。
まず、代数的数を係数とする多項式 f(x)=a_nx^n+\cdots+a_1x+a_0 に対して、係数を変数に置き換えたもの \tilde{f}(y_0,y_1,\ldots,y_n,x)=y_nx^n+\cdots+y_1x+y_0\in\mathbb{Z}[x][y_n,\ldots,y_0] を計算する関数 toMultPoly を作る。 変数の個数が可変なのは y_0,\ldots,y_n の方で、 x は固定なので、 R=\mathbb{Z}[x] を係数環とする多変数多項式 R_n を返す。
toMultPoly :: UniPoly AlgReal -> MultPoly (UniPoly Integer)
toMultPoly 0 = 0
toMultPoly f = sum [multInd i * Scalar (ind^i) | i <- [0..degree' f]]次に、終結式を繰り返し適用する関数 elimN を作る。 この関数は、与えられた代数的実数係数の多項式 f に対して、係数の共役をとったものを掛け合わせて整数係数多項式にしたもの F を返す。
-- Eliminate algebraic numbers in the coefficients by multiplying conjugates
elimN :: UniPoly AlgReal -> UniPoly Integer
elimN f = case loop (toMultPoly f) polynomialsForCoefficients of
Just g -> g
Nothing -> error "elimN: internal error"
where
polynomialsForCoefficients = V.map definingPolynomial (coeff f)
loop :: MultPoly (UniPoly Integer) -> V.Vector (UniPoly Integer) -> Maybe (UniPoly Integer)
loop m v | V.null v = multToScalar m
loop m v = loop (resultant_d (mapCoeff (Scalar . constP) (V.head v)) (multToUni m)) (V.tail v)これを使うと、与えられた代数的実数係数多項式の実根を(重複度込みで)列挙する関数 realRootsA は次のように実装できる:
realRootsA :: UniPoly AlgReal -> [(AlgReal,Int)]
realRootsA f = [ (x,i)
| (g,i) <- yun f
, x <- realRoots (elimN g)
, valueAt x g == 0
]まず、与えられた多項式を無平方分解して重複度 i を決定する。 得られた無平方多項式に対して、終結式を繰り返し適用し (elimN g)、その実根 x を計算する。
無平方分解を先に行なっているのは、「共役を掛け合わせる操作」の段階で重複度が増えることがあるためである。 例えば、重根を持たない f(x)=\sqrt{2}x-\sqrt{3} に対して共役を掛け合わせると、重根を持つ4次の多項式 (2x^2-3)^2 が得られる。
得られた実根が元の多項式の根であるとは限らないので、 g に代入して値が 0 になるかを確かめている。 冒頭の例2で述べたように、これは途方もないコストがかかる。 やってみよう。
(注:#7 と #12 で提示したコードにバグがあったので、律儀にコードを写経している読者の方は各ページの更新情報を見つつ修正しておいて頂きたい。)
$ stack repl
...
... > :set prompt "> "
> let x = ind
> let f = x^2 - scaleP (1 + sqrtQ 2) x - constP (sqrtQ 3)
> :set +s
> realRootsA f
[(AlgReal (UniPoly [9,0,-18,12,-5,4,2,-4,1]) 1 ((-19) % 32) ((-19) % 64),1),(AlgReal (UniPoly [9,0,-18,12,-5,4,2,-4,1]) 1 (19 % 8) (19 % 4),1)]
(865.40 secs, 498,681,647,560 bytes)例2の多項式 x^2-(1+\sqrt{2})x-\sqrt{3} は2個の実根を持つことがわかった。 それはいいのだが、やはり計算時間が長すぎる。 筆者の環境では 865秒、つまり 14 分以上もかかっている。 REPL ではなくネイティブコードにコンパイルすれば多少早くなるだろうし、あるいはマルチコアを活用できるように並列化するという手もあるが、せいぜい定数倍の高速化でしかない。 抜本的な対策を考えよう。
(ちなみに、計算が終わるのはまだマシな方で、前々回の「大きな素数」による因数分解法ではそもそもこの計算ができなかった。)
根のふるい落とし:区間演算
「代数的実数を係数とする多項式に代数的実数を代入して 0 になるか判定する」処理を効率化したい。
#5 区間演算と計算可能実数 で区間演算というのをやったが、これを利用すると、有理数だけを使った大雑把な計算で「計算結果が 0 でない」ということを示せる場合がある。 つまり、区間演算を使って「確実に 0 でない」ことが言えた場合は、高コストな代数的実数の演算を避けることができる。
実装してみよう。
まず、区間が 0 を含むかどうか調べる関数 isCompatibleWithZero を Interval.hs に追加しておく:
-- src/Numeric/AlgebraicReal/Interval.hs に追加
isCompatibleWithZero :: Interval -> Bool
isCompatibleWithZero (Iv a b) = a <= 0 && 0 <= bさっき実装した realRootsA の、 , x <- realRoots (elimN g) と , valueAt x g == 0 の間に、区間演算を使って根をふるい落とす処理を入れる:
realRootsA :: UniPoly AlgReal -> [(AlgReal,Int)]
realRootsA f = [ (x,i)
| (g,i) <- yun f
, x <- realRoots (elimN g)
, let g' = UniPoly $ fmap algRealToCReal $ coeff g
, let CReal y' = valueAt (algRealToCReal x) g'
, isCompatibleWithZero (y' !! 5)
, valueAt x g == 0
]区間演算と言ったが、ここでのコード例では計算可能実数を使って計算し、その後に区間に変換している(どっちでもいい)。
さあやってみよう:
> realRootsA f
[(AlgReal (UniPoly [9,0,-18,12,-5,4,2,-4,1]) 1 ((-19) % 32) ((-19) % 64),1),(AlgReal (UniPoly [9,0,-18,12,-5,4,2,-4,1]) 1 (19 % 8) (19 % 4),1)]
(440.88 secs, 241,342,481,128 bytes)さっきと比べて、実行時間がほぼ半分になった。 これは、 F の実根が 4 個あるうちの 2 個が区間演算によってふるい落とされ、結果として「実際に代入する」のが残りの 2 個だけになったからだと考えられる。
これでだいぶマシになったとも言えるが、そもそも「実際に代入する」ことなく判定できればもっと効率化できるのではないか?
根のふるい落とし:スツルムの定理再び
我々の代数的実数の表し方では、多項式の複数ある根を分離区間によって指定している。 つまり、 F の根 \alpha の分離区間 (a,b) について、 (a,b) にある F の実根は \alpha ただ一つである。
f が F の因数であることを考えると、これは、区間 (a,b) における f の実根は \alpha ただ一つであるか、もしくは区間 (a,b) には f の実根は存在しない、のどちらかが成り立つことを意味する。 #2 で学んだスツルムの定理を使えば、区間 (a,b) における f の実根の個数を正確に数え上げることができる。 この際、 \alpha そのものを f に代入するは必要ない!
この戦略では、代数的実数を係数とする多項式 f のスツルム列の計算をする必要がある。 スツルム列の計算にもコストはかかるが、スツルム列の計算に \alpha は必要なく、 f の係数だけで完結する。 \alpha に比べて f の係数は(代数的実数としては)比較的単純だと考えられるので、 \alpha を使うよりはコストは低くなるだろう。 (例2で言えば、 f(x)=x^2-(1+\sqrt{2})x-\sqrt{3} の根 \alpha は8次の代数的数だが、 f の係数はせいぜい2次の代数的数でしかない。)
realRootsA 関数の , valueAt x g == 0 の部分を次のように変えよう:
, let (x0, x1) = isolatingInterval x
, countRealRootsBetween (fromRational x0) (fromRational x1) g == 1すると、 realRoots 関数は結局、次のようになる:
realRootsA :: UniPoly AlgReal -> [(AlgReal,Int)]
realRootsA f = [ (x,i)
| (g,i) <- yun f
, x <- realRoots (elimN g)
, let g' = unsafeMapCoeff algRealToCReal g
, let CReal y' = valueAt (algRealToCReal x) g'
, isCompatibleWithZero (y' !! 5)
, let (x0, x1) = isolatingInterval x
, countRealRootsBetween (fromRational x0) (fromRational x1) g == 1
]さっきと同じ計算を実行してみよう:
> let f = x^2 - scaleP (1 + sqrtQ 2) x - constP (sqrtQ 3)
(0.05 secs, 361,784 bytes)
> realRootsA f
[(AlgReal (UniPoly [9,0,-18,12,-5,4,2,-4,1]) 1 ((-19) % 32) ((-19) % 64),1),(AlgReal (UniPoly [9,0,-18,12,-5,4,2,-4,1]) 1 (19 % 8) (19 % 4),1)]
(0.64 secs, 293,147,528 bytes)一瞬…! いや、体感できる程度の時間はかかっているのだが、それでも数百秒かかっていた計算が 1 秒未満になったのはすごいことである。
【2018年2月5日 追記】 今回の場合はすでに分離区間が分かっているので、スツルムの定理を使う必要はそもそもなく、単に分離区間の両端で符号が異なっていることを確かめれば良い。 よって、 realRootsA 関数は次のように書き換えられる:
realRootsA :: UniPoly AlgReal -> [(AlgReal,Int)]
realRootsA f = [ (x,i)
| (g,i) <- yun f
, x <- realRoots (elimN g)
, ...
, let (x0, x1) = isolatingInterval x
, signAt (fromRational x0) g * signAt (fromRational x1) g <= 0
]実閉体
我々は代数的実数について
- 四則演算(体)
- 比較演算(順序)
- 代数的実数を係数とする多項式の実根の列挙、特に
- 正の平方根
- 奇数次の実根
を実装した。 ところで、本物の実数においても
- 四則演算(体)
- 比較演算(順序)
- 実数を係数とする多項式の実根の列挙、特に
- 正の平方根
- 奇数次の実根
が行えるし、計算可能実数についても同様の操作ができる(操作が「閉じて」いる)。
今挙げた3つ(代数的実数、計算可能実数、実数)は、実閉体 (real closed field) の例で、特に、代数的実数は最小の実閉体である。
斯くして我々は、計算機上で具体的に取り扱える実閉体を構成したわけである。 実「閉体」ときたら次は代数閉体 (algebraically closed field) だろう。 次回は代数的「実」数を超えて、(複素数の範囲での)代数的数 \overline{\mathbb{Q}} を実装し、この連載の締めくくりとしたい。