#12 多項式の因数分解 その4 整数係数の因数分解
前回までは、有限体係数の多項式因数分解アルゴリズムを扱った。 今回は、整数係数の多項式の因数分解を、有限体(モジュラー)係数に帰着させる。 そうして得られた整数係数多項式の因数分解アルゴリズムを使い、代数的実数の最小多項式を(因数分解して)計算できるようにする。
係数の上限
モジュラー計算での因数分解の結果を整数の世界に持ってくるには、係数の整数としての大きさをあらかじめ見積もっておく必要がある。 つまり、整数係数多項式 f があった時に、その因数 g の係数の絶対値の大きさとしてあり得る最大値を知りたい。
多項式の係数の大きさを見積もるために、多項式のノルムを何種類か導入する。 といっても、ベクトルのノルムとして見たことがある人も多いだろう。
f を \mathbb{C} 係数の多項式とする: f(x)=a_nx^n+\cdots+a_1x+a_0=a_n(x-\alpha_1)\cdots(x-\alpha_n) とする。
1-ノルム: \left\lVert f\right\rVert_1=\sum_{i=0}^n \left\lvert a_i\right\rvert 2-ノルム: \left\lVert f\right\rVert_2=\sqrt{\sum_{i=0}^n \left\lvert a_i\right\rvert^2} \infty-ノルム(max-ノルムとも言う): \left\lVert f\right\rVert_\infty=\max_{0\le i\le n} \left\lvert a_i\right\rvert
ノルムの間の基本的な大小関係として、 \left\lVert f\right\rVert_\infty\le\left\lVert f\right\rVert_2\le\left\lVert f\right\rVert_1\le (n+1)\left\lVert f\right\rVert_\infty, \left\lVert f\right\rVert_2\le\sqrt{n+1}\left\lVert f\right\rVert_\infty が成り立つ(演習:証明せよ)。 つまり、ノルムの違いはせいぜい定数倍の違いでしかなく、どのノルムを使って計算しても係数の最大値(\infty-ノルム)を評価できる。
多項式の根の大きさに関して、 M(f) を M(f):=\left\lvert a_n\right\rvert\cdot\prod_{i=1}^n\max\{1,\left\lvert \alpha_i\right\rvert\} と定義する。 右辺の \prod_{i=1}^n\max\{1,\left\lvert \alpha_i\right\rvert\} は、「f の根のうち絶対値が1よりも大きいもの」の積(の絶対値)である。
多項式 f,g,h\in\mathbb{C}[x] について f=gh ならば M(f)=M(g)M(h) となる。 また、g の根が f の根の部分集合であることに注意すれば、 \frac{M(g)}{\operatorname{lc}(g)}\le\frac{M(f)}{\operatorname{lc}(f)} がわかる。
この M には特に名前はついていないようだが、「多項式の大きさとその因数の大きさを結びつける」重要な役割を担う。
M(f) と f のノルムを結びつける不等式がランダウの不等式 M(f)\le\left\lVert f\right\rVert_2 である。 ランダウの不等式を証明する前に、次の補題を用意する:補題. f\in\mathbb{C}[x], \alpha\in\mathbb{C} に対し、 \left\lVert (x-\alpha)f(x)\right\rVert_2=\left\lVert (\overline{\alpha}x-1)f(x)\right\rVert_2.
証明. f(x)=a_nx^n+\cdots+a_1x+a_0 とおくと、 \left\lVert (x-\alpha)f(x)\right\rVert_2^2 =(1+\left\lvert \alpha\right\rvert^2)\left\lVert f\right\rVert_2^2-2\sum_{i=1}^n \operatorname{Re}(\alpha a_i\overline{a_{i-1}}) =\left\lVert (\overline{\alpha}x-1)f(x)\right\rVert_2^2 となる。 細かい計算は各自で補完してもらいたい。
定理(ランダウの不等式). f\in\mathbb{C}[x] に対し、 M(f)\le\left\lVert f\right\rVert_2.
証明. f の係数と根を f(x)=a_nx^n+\cdots+a_1x+a_0=a_n(x-\alpha_1)\cdots(x-\alpha_n) とおく。 ただし、 \alpha_i は \left\lvert \alpha_1\right\rvert\ge\cdots\ge\left\lvert \alpha_k\right\rvert>1\ge\left\lvert \alpha_{k+1}\right\rvert\ge\cdots\ge\left\lvert \alpha_n\right\rvert という風に絶対値が大きい順に並べ、絶対値が1より大きいものは k 個であるとする。 すると、 M(f) は M(f)=\left\lvert a_n\right\rvert\cdot\prod_{i=1}^k\left\lvert \alpha_i\right\rvert と書ける。
多項式 g\in\mathbb{C}[x] を g(x)=a_n\prod_{i=1}^k(\overline{\alpha_i}x-1)\prod_{i=k+1}^n(x-\alpha_i) とおき、その係数を g(x)=b_nx^n+\cdots+b_0 とおく。 最高次の係数は b_n=a_n\overline{\alpha_1}\cdots\overline{\alpha_k} である。
すると、 M(f)=\left\lvert a_n\alpha_1\cdots\alpha_k\right\rvert=\left\lvert b_n\right\rvert\le\left\lVert g\right\rVert_2 が成り立つ。 あとは、先の補題を使えば \begin{aligned} \left\lVert g\right\rVert_2 =&\left\lVert \frac{g(x)}{\overline{\alpha_1}x-1}(x-\alpha_1)\right\rVert_2 \\ &\vdots \\ =&\left\lVert \frac{g(x)}{(\overline{\alpha_1}x-1)\cdots(\overline{\alpha_k}x-1)}(x-\alpha_1)\cdots(x-\alpha_k)\right\rVert_2 \\ =&\left\lVert f\right\rVert_2 \end{aligned} がわかり、ランダウの不等式が示される。
定理. f(x)=a_nx^n+\cdots+a_1x+a_0\in\mathbb{C}[x], h(x)=b_mx^m+\cdots+b_1x+b_0\in\mathbb{C}[x] で、 h は f を割り切るとする。 このとき、 \left\lVert h\right\rVert_1\le 2^m M(h)\le\left\lvert \frac{b_m}{a_n}\right\rvert 2^m\left\lVert f\right\rVert_2.
証明. まず前半部 \left\lVert h\right\rVert_1\le 2^m M(h) を示す。 h の根を \alpha_1,\ldots,\alpha_m とおく。 h は f を割り切るので、これらは f の根でもある。
h についての根と係数の関係より、 b_i=(-1)^{m-i}b_m\sum_{S\subset{1,\ldots,m},\#S=m-i} \prod_{j\in S} \alpha_j が成り立つ。 ただし、和は m 個の集合から m-i 個を選ぶ組み合わせについてなので、 \binom{m}{m-i}=\binom{m}{i} 個の項からなる。
M の定義より不等式 \left\lvert b_m\right\rvert\prod_{j\in S} \left\lvert \alpha_j\right\rvert\le M(h) が成り立つので、 \left\lvert b_i\right\rvert\le\left\lvert b_m\right\rvert\sum_{S} \prod_{j\in S} \left\lvert \alpha_j\right\rvert \le\binom{m}{i}M(h) が言える。
よって、示したい不等式の前半部が得られる: \left\lVert h\right\rVert_1\le\sum_{i=0}^m\left\lvert b_i\right\rvert\le\sum_{i=0}^m\binom{m}{i}M(h)=2^m M(h).
不等式の後半部分 2^m M(h)\le\left\lvert \frac{b_m}{a_n}\right\rvert 2^m\left\lVert f\right\rVert_2 は、 M についての基本性質 \frac{M(h)}{\operatorname{lc}(h)}\le\frac{M(f)}{\operatorname{lc}(h)} およびランダウの不等式から従う: 2^m M(h)\le\left\lvert \frac{b_m}{a_n}\right\rvert 2^m M(f)\le\left\lvert \frac{b_m}{a_n}\right\rvert 2^m\left\lVert f\right\rVert_2.
系 (Mignotte’s bound). f,g,h を整数係数多項式とし、 n=\deg f\ge 0, m=\deg g, k=\deg h とする。 gh が f を(整数係数で)割り切るならば、
- \left\lVert g\right\rVert_\infty\left\lVert h\right\rVert_\infty\le\left\lVert g\right\rVert_2\left\lVert h\right\rVert_2\le \left\lVert g\right\rVert_1\left\lVert h\right\rVert_1\le 2^{m+k}\left\lVert f\right\rVert_2 \le\sqrt{n+1}\cdot 2^{m+k}\left\lVert f\right\rVert_\infty
- \left\lVert h\right\rVert_\infty\le\left\lVert h\right\rVert_2\le \left\lVert h\right\rVert_1\le 2^k\left\lVert f\right\rVert_2 \le 2^k\left\lVert f\right\rVert_1, \left\lVert h\right\rVert_\infty\le\left\lVert h\right\rVert_2\le \left\lVert h\right\rVert_1\le 2^k\left\lVert f\right\rVert_2 \le\sqrt{n+1}\cdot 2^k\left\lVert f\right\rVert_\infty
が成り立つ。
証明. これらの主張の核心部は
- \left\lVert g\right\rVert_1\left\lVert h\right\rVert_1\le 2^{m+k}\left\lVert f\right\rVert_2
- \left\lVert h\right\rVert_1\le 2^k\left\lVert f\right\rVert_2
で、残りはノルムについての基本的な不等式から導かれる。
i. について: \begin{aligned} \left\lVert g\right\rVert_1\left\lVert h\right\rVert_1 &\le 2^{m+k}M(g)M(h) \\ &=2^{m+k}M(gh) \\ &\le\left\lvert \frac{\operatorname{lc}(gh)}{\operatorname{lc}(f)}\right\rvert 2^{m+k}\left\lVert f\right\rVert_2 \\ &\le 2^{m+k}\left\lVert f\right\rVert_2 \end{aligned} 1行目の不等式は定理の前半より成り立つ。 2行目の等式は、 M の基本性質 M(g)M(h)=M(gh) である。 3行目の不等式は、定理の後半である。 gh が f を整数係数で割り切ることに注意すれば \left\lvert \frac{\operatorname{lc}(gh)}{\operatorname{lc}(f)}\right\rvert\le 1 なので、4行目の不等式を得る。
ii. については、 g=1 として i. を適用すれば良い。
整数係数の因数分解(big prime 版)
整数係数の因数分解アルゴリズムへの入力は、無平方原始多項式とする。 無平方とは限らない多項式を入力とする場合は、先に(#8 でやった)無平方分解を行えば良い。
このアルゴリズムでは有限体 \mathbb{F}_p での因数分解アルゴリズムを利用するわけなので、まずその素数を決定する。 後で整数に戻すことを考え、素数 p は係数の上限の2倍を超えるように選ぶ。 そのほかにも注意点があり、 mod p での像 \overline{f}\in\mathbb{F}_p が無平方となるような素数 p を選ばなければならない。
f はすでに無平方と仮定しているのに、改めて「mod p で無平方」とはどういうことか。 例えば、整数係数多項式 x^2+1\in\mathbb{Z}[x] は無平方だが、それを \mathbb{F}_2 に持っていったもの x^2+1\in\mathbb{F}_2[x] は無平方ではない。 なぜなら、 mod 2 では x^2+1=(x+1)^2 となるからだ。 このように、整数係数多項式が無平方でも、それを mod p の世界に持っていったものは無平方とは限らないので、素数を選ぶ際に気をつけなければならない。
整数係数多項式を mod p で見たときに無平方かどうか確かめるには、#6 で見た判別式が利用できる。 整数の世界での D(f)\in\mathbb{Z} が mod p で 0 になれば、その多項式 f は mod p で重根を持つ(無平方にならない)。 まあ、わざわざ判別式を計算するよりは、実際に \mathbb{F}_p[x] で \gcd(\overline{f},\overline{f'})=1 となるかを計算するので十分であろう。
(このアルゴリズムでは、素数 p を「係数の上限の2倍を超えるように選ぶ」ので、結構大きな素数を使うことになる。 この他に、ヘンゼルの補題を利用するアルゴリズムもあるが、今回は紹介しない。)
さて、なんとか頑張って、f が mod p でも無平方となる十分大きな奇素数 p を見つけたとしよう。 Cantor-Zassenhaus の方法 でも Berlekamp の方法 でも良いが、 f の mod p での像 \overline{f}\in\mathbb{F}_p を因数分解する: \overline{f}=\overline{\operatorname{lc}(f)}g_1\cdots g_r\in\mathbb{F}_p[x] ただし、 g_i\in\mathbb{F}_p[x] は既約なモニック多項式とする。 これまでに紹介した有限体上の因数分解アルゴリズムはモニック多項式を対象とするため、 \overline{f} は一旦モニック多項式に変換してから因数分解する。
あとは、この g_i の係数を (-p/2,p/2) の範囲で整数に戻せば f の因数分解が得られる…という風には、残念ながらいかない。
例 f(x)=x^3-1 の因数分解を考える。 整数係数での因数分解はもちろん、 x^3-1=(x-1)(x^2+x+1) である。 f の因数の係数の上限は、例えば \sqrt{3+1}\cdot 2^3\cdot\left\lVert f\right\rVert_\infty=16 と計算できる。 よって、 2\cdot 16+1=33 よりも大きな素数 p を選んでやれば、 mod p で計算した因数の係数を整数に戻せるはずである。 というわけで p=37 を選んでみると、 \overline{f}\in\mathbb{F}_{37} は x^3-1=(x-1)(x-10)(x+11) と因数分解される。 つまり、整数係数での既約多項式 x^2+x+1 が mod 37 では「より細かく」 (x-10)(x+11) と因数分解されてしまい、 x-10 や x+11 を整数の世界に戻してやっても元の x^3-1 の因数にはならない。
このような都合の悪い現象があるので、整数係数多項式 f の mod n での因数分解の結果を整数の世界に戻す際には、「mod n での既約因数のいくつかの組み合わせを考え、その積を整数の世界に戻して実際に f を割り切るか試す」というステップが必要になる。
例 f(x)=x^3-1 を mod 37 で因数分解した結果は f(x)=(x-1)(x-10)(x+11) である。 f の整数での因数分解を考える際には、 \{x-1,x-10,x+11\} のいくつかの組み合わせの積 \begin{gathered} x-1, x-10, x+11, \\ (x-1)(x-10)=x^2-11x+10, \\ (x-1)(x+11)=x^2+10x-11, \\ (x-10)(x+11)=x^2+x+1, \\ (x-1)(x-10)(x+11)=x^3-1 \end{gathered} のそれぞれに対して、「整数の世界で f を割り切るか」を考えなくてはならない。 (なお、この例では、 x-1 が f を割り切るとわかった時点で、残る x-10 と x+11 の組み合わせ x-10,x+11,(x-10)(x+11)=x^2+x+1 だけを考えればよくなるので、7通り全てを試す必要はない。)
「あらゆる組み合わせを試す」というのはいかにも効率が悪そうであるが、今回はこの方法で行く。 余裕があればこの問題の回避策も紹介したいが、この連載の本題である代数的数の扱いがひと段落した後になるだろう。
まとめると、アルゴリズムは次のようになる:
入力は無平方原始多項式 f で、最高次の係数は正とする。
- 因数の係数の上限 B=\sqrt{n+1}\cdot 2^n\left\lVert f\right\rVert_\infty\cdot\operatorname{lc}(f) を計算する。 B は Mignotte’s bound をさらに \operatorname{lc}(f) 倍したものである。 あるいは、 \operatorname{lc}(f)f に対する Mignotte’s bound と言っても良いかもしれない。
- 適切な素数 p を見つける。
- 2B+1 よりも大きな素数 p を選ぶ。
- f の mod p での像 \overline{f} が無平方かどうか確かめる。 つまり、 \gcd(\overline{f},\overline{f'}) が 1 となるかを見る。 無平方でなかった場合は、 i. に戻って別の素数を選ぶ。
- 有限体上の因数分解アルゴリズムを使い、 \overline{f}\in\mathbb{F}_p[x] を因数分解する。 つまり、既約なモニック多項式 g_1,\ldots,g_r\in\mathbb{F}_p[x] によって \overline{f}=\overline{\operatorname{lc}(f)}g_1\cdots g_r と表す。
- T:=\{1,\ldots,r\}, f^*:=f とおく。 k=1,2,\ldots について、以下を順番に実行する:
- 2k>\#T ならば f^* は既約であり(後述)、アルゴリズムを終了する。
- T の k 元部分集合 S (S\subset T,\#S=k) それぞれについて、以下を実行する:
- g_1,\ldots,g_r のうち、 S に対応するものの積を取る:g:=\overline{\operatorname{lc}(f^*)}\prod_{i\in S} g_i. 残り T\setminus S に対しても積を取る:h:=\overline{\operatorname{lc}(f^*)}\prod_{i\in T\setminus S} g_i.
- g, h を (-p/2,p/2) の範囲で整数係数に直す:それぞれ g^*\in\mathbb{Z}[x], h^*\in\mathbb{Z}[x] とおく。
- \left\lVert g^*\right\rVert_1\left\lVert h^*\right\rVert_1<B ならば、 g^*h^*=\operatorname{lc}(f^*)f^* である(後述)。 \operatorname{pp}(g^*) はアルゴリズムの結果となるべき f の因数である。 T:=T\setminus S, f^*:=\operatorname{pp}(h^*) とおき、 ii. に戻る。
以下、アルゴリズムに対する補足説明をする。 多項式 f が mod p で m 個の既約因数に分解する時、 \mu という記号を使って \mu(f)=m と表すことにする。 この記号を使うと、アルゴリズムの 3. の段階では \mu(f)=r であり、 4. では f^* の既約因数 g に対して \mu(g)\ge k を仮定している。
アルゴリズムの不変条件として、
- \mu(f^*)=\#I,
- f^* の任意の既約因数 g に対して \mu(g)\ge k,
- \mathbb{F}_p[x] において \overline{f^*}=\overline{\operatorname{lc}(f^*)}\prod_{i\in T} g_i,
- f^* は f の因数
などが成り立つ。
アルゴリズムの終了条件について。 f^* が非自明な g^*h^* に分解するとしよう。 不変条件より k\le\mu(g^*), k\le\mu(h^*) が成り立つので、 2k\le\mu(g^*)+\mu(h^*)=\mu(g^*h^*)=\mu(f^*)=\#I である。 対偶を取れば、「2k>\#I であれば f^* は既約である」となり、アルゴリズム中に書いた終了条件が正しいことがわかる。 (#10 で見た次数別因数分解アルゴリズムの終了条件も、似たような議論である。)
4.ii.c. の「\left\lVert g^*\right\rVert_1\left\lVert h^*\right\rVert_1<B ならば g^*h^*=\operatorname{lc}(f^*)f^* である」について。 まず、アルゴリズムの不変条件と、 g^*, h^* の選び方より、 g^*h^*\equiv\operatorname{lc}(f^*)f^*\mod{p} が成り立つ。 あとは、両者の係数の絶対値が p/2 未満であることを確かめれば、この合同式が真の(\mathbb{Z}[x] での)等式であることが言える。 左辺については、ノルムの性質を使えば \left\lVert g^*h^*\right\rVert_\infty\le\left\lVert g^*h^*\right\rVert_1\le\left\lVert g^*\right\rVert_1\left\lVert h^*\right\rVert_1\le B<p/2 とわかる。 右辺については、 \operatorname{lc}(f^*)f^* が \operatorname{lc}(f)f の因数であることに注意すれば、 B の取り方よりわかる。 よって両辺共に係数の絶対値が p/2 未満であることが言え、合同式は等式となる。
実装
外部パッケージの利用
実装には「指定された範囲の素数を列挙する」操作が必要である。 もちろん自分で実装することもできるが、面倒なので、既存のライブラリーを利用することにする。 Haskell で素数を扱うライブラリーはいくつかあるようだが、ここでは arithmoi パッケージを利用する。
arithmoi パッケージでは、「指定された範囲の素数を列挙する」操作には、 Math.NumberTheory.Primes.Sieve モジュールにある
-- 素数のリスト
primes :: [Integer]
-- 与えられた整数 n に対して、 n 以上の素数のリストを返す
sieveFrom :: Integer -> [Integer]が使えそうである。
「係数の上限」で整数の平方根が登場しているので、それを計算する関数もあると良さそうである。 arithmoi パッケージでは Math.NumberTheory.Powers.Squares モジュールにそういう関数が用意されている。
-- 非負整数 n に対して、 r * r <= n となる最大の r を返す
integerSquareRoot :: Integral a => a -> aこれまでは有限体の計算の際には REPL 上で(DataKinds 拡張を使い) f :: UniPoly (PrimeField 37) という風に法となる素数を直接記述していたが、今回のアルゴリズムで使う素数は f に依存して実行時に決まる。 Haskell において実行時の値に依存した型レベル自然数を作るには、#9 でも触れたように、reflection パッケージを使う。
具体的には、 Data.Reflection モジュール で提供されている reifyNat 関数を使う:
-- 与えられた自然数 (Integer) を型レベル自然数 (KnownNat n) の Proxy として関数に渡す
reifyNat :: forall r. Integer -> (forall n. KnownNat n => Proxy n -> r) -> r例えば、 reifyNat 37 (\proxy -> ...) と書けば、渡した関数の引数 proxy が Proxy 37 型として呼び出される。
というわけで、 algebraic-real.cabal に arithmoi と reflection を追加しておく:
build-depends: base >= 4.7 && < 5
...
, array
, arithmoi
, reflectionコード
今回の因数分解アルゴリズムは src/Numeric/AlgebraicReal/Factor/BigPrime.hs に記述する。
module Numeric.AlgebraicReal.Factor.BigPrime where
import Prelude hiding (toInteger)
import Numeric.AlgebraicReal.UniPoly
import Numeric.AlgebraicReal.Factor.CantorZassenhaus (factorCZ)
import Data.FiniteField (PrimeField,char,toInteger)
import System.Random (RandomGen,getStdRandom)
import qualified Data.Vector as V
import Control.Monad (guard)
import Data.Proxy (Proxy)
import GHC.TypeLits (KnownNat)
import Data.Reflection (reifyNat)
import Math.NumberTheory.Powers.Squares (integerSquareRoot)
import Math.NumberTheory.Primes.Sieve (sieveFrom)
import Control.Arrow (first,second)
-- 1-norm of coefficients
oneNorm :: (Ord a, Num a) => UniPoly a -> a
oneNorm f = V.sum $ V.map abs $ coeff f
-- max-norm of coefficients
maxNorm :: (Ord a, Num a) => UniPoly a -> a
maxNorm f = V.maximum $ V.map abs $ coeff f
factorCoefficientBound :: UniPoly Integer -> Integer
factorCoefficientBound f = (integerSquareRoot (n + 1) + 1) * 2^n * maxNorm f -- or, 2^n * oneNorm f
where n = fromIntegral (degree' f)まず、1-ノルムを計算する関数 oneNorm, max-ノルム (\infty-ノルム) を計算する関数 maxNorm を適当にでっち上げる。 それを使って、多項式の因数の上限を計算する関数 factorCoefficientBound を書く。
-- @partitions n s@ returns all possible partitions @(t,u)@ with @t ++ u == s@ (as a set) and @length t == n@
partitions :: Int -> [a] -> [([a],[a])]
partitions 0 [] = [([],[])]
partitions n [] = []
partitions n (x:xs) = map (first (x:)) (partitions (n-1) xs) ++ map (second (x:)) (partitions n xs)後の操作で「n 個の集合から k 個を取り出す組み合わせを全て試す」という操作が必要になるので、そういう操作を実装しておく。 ただし、集合の代わりにリストを使っており、また、選ばれなかった n-k 個もリストとして返している。 実行例としては、例えば「集合 \{1,2,3,4\} から2個取り出す」であれば
> partitions 2 [1,2,3,4]
[([1,2],[3,4]),([1,3],[2,4]),([1,4],[2,3]),([2,3],[1,4]),([2,4],[1,3]),([3,4],[1,2])]となる。
コードの続きを見ていこう。
primeFieldFromInteger :: (KnownNat p) => Proxy p -> Integer -> PrimeField p
primeFieldFromInteger _ = fromInteger
-- converts a @PrimeField p@ value into integer in (-p/2,p/2]
toInteger' :: (KnownNat p) => PrimeField p -> Integer
toInteger' x | x' * 2 <= p = x'
| otherwise = x' - p
where p = char x
x' = toInteger x整数を有限体 PrimeField p に変換する関数 primeFieldFromInteger を用意する。 やっていることはただの fromInteger なのだが、法 p を Proxy で明示できるのがポイントである。
有限体 PrimeField p を (-p/2,p/2] の範囲で整数に戻す関数 toInteger' も用意する。 Data.FiniteField モジュールで提供される toInteger 関数は、値の範囲が [0,p) である。
次がいよいよ、アルゴリズムの核心部である。
-- Input: nonzero, primitive, squarefree, leading coefficient > 0
factorInt :: (RandomGen g) => UniPoly Integer -> g -> ([UniPoly Integer], g)
factorInt f =
let bound = factorCoefficientBound f * leadingCoefficient f
p:_ = filter (\p -> reifyNat p coprimeModP f (diffP f)) $ sieveFrom (2 * bound + 1)
in reifyNat p factorWithPrime bound f
factorIntIO :: UniPoly Integer -> IO [UniPoly Integer]
factorIntIO f = getStdRandom (factorInt f)
coprimeModP :: (KnownNat p) => Proxy p -> UniPoly Integer -> UniPoly Integer -> Bool
coprimeModP proxy f g =
let f' = mapCoeff (primeFieldFromInteger proxy) f
g' = mapCoeff (primeFieldFromInteger proxy) g
in degree (gcdP f' g') == Just 0factorInt は整数係数の無平方原始多項式(と乱数生成器)を受け取り、それを因数分解したものを返す関数である。
まず、因数の係数の限界 bound を計算する。 次に、「適切な」素数 p を選ぶ。 係数の限界 bound の2倍を超える範囲から、 f が無平方となるように選ぶ。
mod p で無平方であることの判定は coprimeModP 関数を使う。 有限体を使って GCD を計算するので、 reifyNat で素数を型レベル自然数として coprimeModP を呼び出す。
factorIntIO 関数は、 factorInt でグローバルな乱数生成器を使うようにした版で、 IO モナドの関数である。 ここでもしも結果が乱数の状態に依存しないのであれば unsafePerformIO を使うことも検討したかもしれないが、入力が同じでも得られる因数のリストの順番はランダムなため、 unsafePerformIO は使うべきではない。
素数 p が決まったら、 reifyNat で factorWithPrime 関数を呼び出す:
-- p must be prime
factorWithPrime :: (KnownNat p, RandomGen g) => Proxy p -> Integer -> UniPoly Integer -> g -> ([UniPoly Integer], g)
factorWithPrime proxy bound f gen =
let f' = toMonic $ mapCoeff (primeFieldFromInteger proxy) f -- :: UniPoly (PrimeField p)
(modularFactors, gen') = factorCZ f' gen
in (factorCombinations bound 1 f modularFactors, gen')f を有限体 \mathbb{F}_p 上の多項式とみなし、さらにモニック多項式に直したものを f' とおく。 そうしたら、前々回実装した Cantor-Zassenhaus のアルゴリズム factorCZ により f' を因数分解する。 mod p での因数のリストは modularFactors 変数に入る。 それが終わったら、「因数の組み合わせを試す」 factorCombinations 関数を呼び出す:
factorCombinations :: (KnownNat p) => Integer -> Int -> UniPoly Integer -> [UniPoly (PrimeField p)] -> [UniPoly Integer]
factorCombinations bound k f [] = [] -- f must be 1
factorCombinations bound k f modularFactors
| 2 * k > length modularFactors = [f] -- f is already irreducible
| otherwise = case tryFactorCombinations of
[] -> factorCombinations bound (k+1) f modularFactors
(g,h,rest):_ -> g : factorCombinations bound k h rest
where tryFactorCombinations = do
(s,rest) <- partitions k modularFactors
-- length s == k, s ++ rest == modularFactors (as a set)
let lc_f = fromInteger (leadingCoefficient f)
g = mapCoeff toInteger' (lc_f * product s)
h = mapCoeff toInteger' (lc_f * product rest)
guard (oneNorm g * oneNorm h <= bound)
return (primitivePart g, primitivePart h, rest)factorCombinations 関数は、 f の因数は modularFactors の k 個以上の組み合わせからなると仮定して、 f を因数分解する(最初は k=1 から始める)。 中身は、さっき解説したとおりである。
コードを書き終わったら、 algebraic-real.cabal に今回のモジュール名 Numeric.AlgebraicReal.Factor.BigPrime を追加する:
exposed-modules: Numeric.AlgebraicReal.UniPoly
...
, Numeric.AlgebraicReal.Factor.Berlekamp
, Numeric.AlgebraicReal.Factor.BigPrime試す
いつものように stack repl を使って試してみよう。
$ stack repl
...
......> :set prompt "> "
> :m + System.Random
> setStdGen (mkStdGen 413941056)
> let x = indまずは x^2-1, x^3-2x+1 などの簡単な多項式を因数分解してみよう:
> factorIntIO $ x^2 - 1
[UniPoly [1,1],UniPoly [-1,1]]
> factorIntIO $ x^3 - 2*x + 1
[UniPoly [-1,1],UniPoly [-1,1,1]]うまくいっているようである。 次に、 x^{11}-1 や x^{20}-1 など、もっと次数の高い多項式を分解してみよう:
> factorIntIO $ x^11 - 1
[UniPoly [-1,1],UniPoly [1,1,1,1,1,1,1,1,1,1,1]]
> factorIntIO $ x^20 - 1
[UniPoly [1,1],UniPoly [-1,1],UniPoly [1,0,1],UniPoly [1,1,1,1,1],UniPoly [1,-1,1,-1,1],UniPoly [1,0,-1,0,1,0,-1,0,1]]
> factorIntIO $ (x^3+1)*(x^4-2)*(x^7+6*x^6-x^2+3)
[UniPoly [1,1],UniPoly [-2,0,0,0,1],UniPoly [1,-1,1],UniPoly [3,0,-1,0,0,0,6,1]]いずれも、数秒もかからずに因数分解できたのではないだろうか。 #8 での Kronecker の方法での所要時間と比べて欲しい。
調子に乗って、どこまでいけるかやってみよう:
> factorIntIO $ x^50 - 1
[UniPoly [1,1],UniPoly [-1,1],UniPoly [1,1,1,1,1],UniPoly [1,-1,1,-1,1],UniPoly [1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1],UniPoly [1,0,0,0,0,-1,0,0,0,0,1,0,0,0,0,-1,0,0,0,0,1]]x^{50}-1 の因数分解には、筆者の環境では 37.5 秒かかった。 x^{100}-1 だとどうなるか:
> factorIntIO $ x^100 - 1
<interactive>: Out of memoryOut of memory が出て、 REPL が終了してしまった。
なぜこんなことになってしまったのか。 まず、 x^{100}-1 に対する係数の上限の見積もり factorCoefficientBound (x^100-1) は 13944156602510523416463735259136 となり、使うべき素数はその2倍+1よりも大きいもの、となる。 実は、今回利用している arithmoi パッケージの素数列挙関数は、これほど大きな素数には対応していない(ドキュメントを参照)。 したがって、100次の多項式を因数分解するには、「大きな素数」を使わない方法が必要である。 だが、その方法を解説するにはまだまだ準備が必要なため、今回は取り上げない。
最小多項式の計算
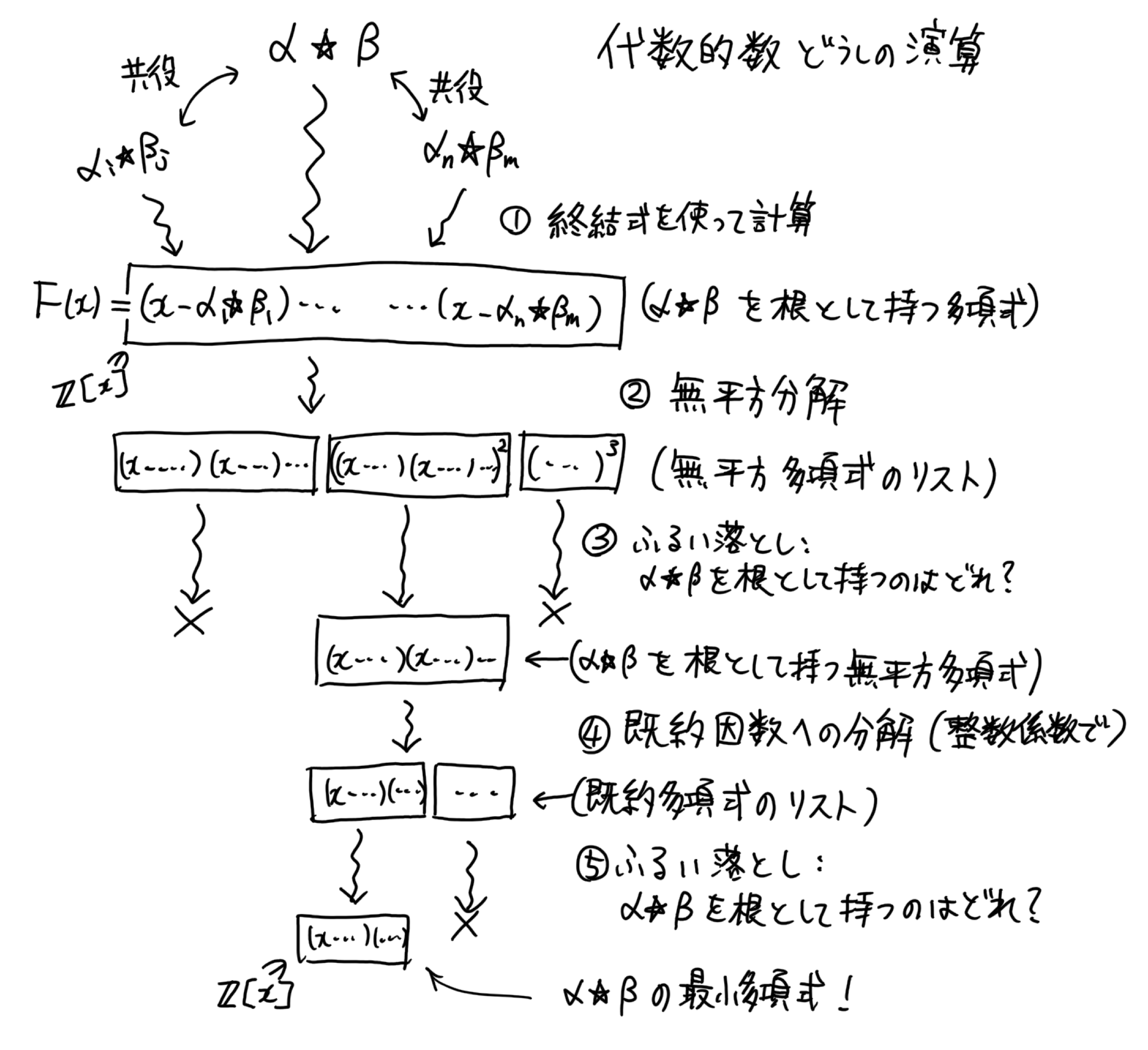
そもそもなんで多項式の因数分解の実装に取り組んでいたのかというと、 #6 で見たように、代数的数の定義多項式を因数分解しないと演算に伴って次数が不必要に増大するからだった。 今、整数係数多項式のそこそこ実用的な因数分解アルゴリズムの実装を手に入れたので、早速代数的数の実装に応用してみよう。
代数的実数の実装は src/Numeric/AlgebraicReal/AlgReal.hs にあったので、そこに再び手を加える。
モジュールの import 部に、次の3行を加える:
import Numeric.AlgebraicReal.Factor.SquareFree
import Numeric.AlgebraicReal.Factor.BigPrime
import System.IO.Unsafe (unsafePerformIO)mkAlgReal 関数は、次の関数で置き換える:
-- | 与えられた既約多項式と、分離区間 (a,b] から、代数的実数を構築する。
mkAlgRealWithIrreduciblePoly :: UniPoly Integer -> Rational -> Rational -> AlgReal
mkAlgRealWithIrreduciblePoly f a b
-- 区間が空の場合はエラー
| b <= a = error "mkAlgReal: empty range"
-- 最小多項式が1次の場合は、ただの有理数
| degree f == Just 1 = case V.toList (coeff f) of
[a,b] -> FromRat (-a % b)
-- 区間の符号が確定したものをデータ構築子として使う
| otherwise = AlgReal f s a' b'
where s | signAtZQ b f > 0 = 1
| signAtZQ b f < 0 = -1
| otherwise = error "f is not irreducible"
Just (Iv a' b') = find (\(Iv x y) -> 0 < x || y < 0) (intervalsWithSign f s a b)mkAlgRealWithCReal 関数の実装は次のように置き換える:
-- | 与えられた多項式と、その根に収束する計算可能実数から、代数的実数を構築する。
mkAlgRealWithCReal :: UniPoly Integer -> CReal -> AlgReal
mkAlgRealWithCReal f (CReal xs) = sieve squareFreeFactors xs
where
squareFreeFactors :: [UniPoly Integer]
squareFreeFactors = map fst $ yun $ primitivePart f
sieve :: [UniPoly Integer] -> [Interval] -> AlgReal
sieve [] _ = error "invalid real number"
sieve [g] xs = sieve2 (unsafePerformIO (factorIntIO g)) xs
sieve gs (x@(Iv a b):xs) = sieve (filter (\g -> isCompatibleWithZero (valueAtZ x g)) gs) xs
sieve2 :: [UniPoly Integer] -> [Interval] -> AlgReal
sieve2 [] _ = error "invalid real number"
sieve2 [g] xs = case dropWhile (\(Iv a b) -> countRealRootsBetweenZQ a b g >= 2) xs of
Iv a b : _ -> mkAlgRealWithIrreduciblePoly g a b
sieve2 gs (x@(Iv a b):xs) = sieve2 (filter (\g -> isCompatibleWithZero (valueAtZ x g)) gs) xs
isCompatibleWithZero :: Interval -> Bool
isCompatibleWithZero (Iv a b) = a <= 0 && 0 <= b【1月23日 修正】 公開時に載せたコードでは、先に完全な因数分解をしてから区間演算で絞り込むということをやっていたが、その実装では不必要な因数分解を行おうとしてメモリを食い潰すという不具合があった。 そこで、無平方分解の時点で因数を絞り込み、その後に完全な因数分解を行うようにした。
何をやっているかというと、与えられた多項式を因数分解し、その中から与えられた計算可能実数を根に持つものを絞り込む(sieve 関数)。 絞り込みが完了したら、実根が一意になるように区間を狭めていく。
mkAlgRealWithInterval 関数は、削除して構わない。
今度は、「与えられた多項式の実根を列挙する」 realRoots 系の関数に手を加える。 まず、これまでの関数は根の重複度を考慮していなかった。 そこで、重複度も返す版の関数を追加する:
realRootsM :: UniPoly Integer -> [(AlgReal,Int)]
realRootsBetweenM :: UniPoly Integer -> ExtReal Rational -> ExtReal Rational -> [(AlgReal,Int)]実装は次のようになる:
realRoots :: UniPoly Integer -> [AlgReal]
realRoots f = map fst (realRootsM f)
realRootsM :: UniPoly Integer -> [(AlgReal,Int)]
realRootsM f = realRootsBetweenM f NegativeInfinity PositiveInfinity
-- 多項式の実根のうち、指定された区間にあるものを、重複度込みで返す
realRootsBetweenM :: UniPoly Integer -> ExtReal Rational -> ExtReal Rational -> [(AlgReal,Int)]
realRootsBetweenM f lb ub
| f == 0 = error "realRoots: zero" -- 多項式 0 の実根を求めようとするのはエラー
| degree' f == 0 = [] -- 多項式が 0 でない定数の場合、実根はない
| otherwise = sortOn fst $ do
(g,i) <- yun (primitivePart f) -- f を無平方分解する
h <- unsafePerformIO (factorIntIO g) -- g を因数分解する
let seq = negativePRS h (diffP h) -- h のスツルム列
bound = rootBound h -- 根の限界
lb' = clamp (-bound) bound lb -- 与えられた区間の下界を有理数にしたもの
ub' = clamp (-bound) bound ub -- 与えられた区間の上界を有理数にしたもの
a <- bisect h seq (lb',varianceAtZQX lb seq) (ub',varianceAtZQX ub seq)
return (a,i)
where
-- 実装のキモ:与えられた区間の実根を列挙する。区間の端点におけるスツルム列の符号の変化も受け取る。
bisect :: UniPoly Integer -> [UniPoly Integer] -> (Rational,Int) -> (Rational,Int) -> [AlgReal]
bisect f seq p@(a,i) q@(b,j)
| i <= j = [] -- 区間に実根が存在しない場合
| i == j + 1 = [mkAlgRealWithIrreduciblePoly f a b] -- 区間にちょうど一個の実根が存在する場合
| otherwise = bisect f seq p r ++ bisect f seq r q -- それ以外:複数個の実根が存在するので区間を分割する
where c = (a + b) / 2
r = (c,varianceAtZQ c seq)
realRootsBetween :: UniPoly Integer -> ExtReal Rational -> ExtReal Rational -> [AlgReal]
realRootsBetween f lb ub = map fst (realRootsBetweenM f lb ub)【1月23日 修正】 realRootsBetweenM の実装で、与えられた多項式を原始多項式に変換するようにした。
代数的実数に対する演算の部分も変える。
【2018年2月4日 修正】足し算と引き算の実装を修正。
足し算:
FromRat k + AlgReal f s a b = mkAlgRealWithIrreduciblePoly (primitivePart $ fst $ homogeneousCompP f (definingPolynomial (FromRat k)) (denominator k)) (a + k) (b + k)
...
x + y = mkAlgRealWithCReal (resultant_poly f_x_y g) (algRealToCReal x + algRealToCReal y)引き算:
FromRat k - AlgReal f s a b = mkAlgRealWithIrreduciblePoly (primitivePart $ fst $ homogeneousCompP f (- definingPolynomial (FromRat k)) (denominator k)) (k - b) (k - a)
AlgReal f s a b - FromRat k = mkAlgRealWithIrreduciblePoly (primitivePart $ fst $ homogeneousCompP f (definingPolynomial (FromRat (-k))) (denominator k)) (a - k) (b - k)
x - y = mkAlgRealWithCReal (resultant_poly f_x_y g) (algRealToCReal x - algRealToCReal y)掛け算:
x * y = mkAlgRealWithCReal (resultant_poly y_f_x_y g) (algRealToCReal x * algRealToCReal y)これで、「最小多項式を計算して次数の不必要な増加を防ぐ」代数的実数の実装になったはずである。 早速試してみよう。
試す
stack repl で、いつものようにコマンドを打ち込む。
$ stack repl
...
......> :set prompt "> "
> :m + System.Random
> setStdGen (mkStdGen 23528935713)ここから先は、 #6 での実行結果と比較して欲しい。
> sqrtQ 2
AlgReal (UniPoly [-2,0,1]) 1 (3 % 4) (3 % 2)
> 2 :: AlgReal
FromRat (2 % 1)
> (sqrtQ 2)^2
FromRat (2 % 1)\sqrt{2} を2乗すると2となることが確認でき、しかも、表示まで同じとなった! この表示 FromRat (2 % 1) を得るためにこの連載の6回分が費やされたと言っても過言ではない。
> sqrtQ 2 + sqrtQ 8
AlgReal (UniPoly [-18,0,1]) 1 (27 % 8) (39 % 8)
> 2 * sqrtQ 2
AlgReal (UniPoly [-8,0,1]) 1 (3 % 2) (3 % 1)
> sqrtQ 8
AlgReal (UniPoly [-8,0,1]) 1 (9 % 4) (9 % 2)2\sqrt{2} と \sqrt{8} の表示が(区間の部分を除いて)一致していることがわかる。
もっと複雑な代数的数も扱ってみよう。
> let x = ind
> let [a0,a1,a2,a3] = realRoots $ (x-4)*(x-3)*(x-2)*(x+3)+1
> a0
AlgReal (UniPoly [-71,54,-1,-6,1]) (-1) ((-9) % 2) ((-9) % 4)
> a1
AlgReal (UniPoly [-71,54,-1,-6,1]) 1 (9 % 8) (9 % 4)
> a2
AlgReal (UniPoly [-71,54,-1,-6,1]) (-1) (9 % 4) (27 % 8)
> a3
AlgReal (UniPoly [-71,54,-1,-6,1]) 1 (27 % 8) (9 % 2)#6 での結果よりもスッキリしているように見えるのは、 #7 で整数係数多項式を使うようにしたためである。
根どうしの和を計算してみよう。
> a0 + a1
AlgReal (UniPoly [-36,18,33,-12,1]) (-1) ((-27) % 16) ((-27) % 32)#6 では係数膨張が起こったが、演習問題をきちんとこなしていれば解決済みのはずである。
根と係数の関係を確かめてみよう。
> a0 + a1 + a2 + a3
FromRat (6 % 1)筆者の環境では1秒ほどかかった。
> a0 * a1 * a2 * a3
Killed: 9筆者の環境では REPL がメモリを食いつぶして頓死してしまった。 どうやらまだバグが潜んでいるようであるが、今回はここで筆を置くことにする。
【1月23日 更新】 コードを更新し、メモリを食いつぶさないようにした:
> a0 * a1 * a2 * a3
FromRat ((-71) % 1)