#13 多項式の因数分解 その5 Hensel の補題
前回、「大きな素数」を使う整数係数多項式の因数分解アルゴリズムを実装し、それを使って代数的実数の最小多項式を計算できるようにした。
簡単な代数的実数の計算であれば、前回の因数分解アルゴリズムはうまくいく。 しかし、ある程度複雑な数を扱おうとすると、アルゴリズムの破綻が見えてくる。
例 多項式 f(x)=x^8-4x^7+2x^6+4x^5-5x^4+12x^3-18x^2+9 の実根のうち最小のもの \alpha について、 \alpha^2-(1+\sqrt{2})\alpha-\sqrt{3} を計算しよう。
> let [a0,a1,a2,a3] = realRoots (x^8-4*x^7+2*x^6+4*x^5-5*x^4+12*x^3-18*x^2+9)
> (a0 - 1 - sqrtQ 2) * a0 - sqrtQ 3
*** Exception: integerSquareRoot: negative argument
CallStack (from HasCallStack):
error, called at ./Math/NumberTheory/Powers/Squares.hs:50:19 in arithmoi-0.6.0.1-5biqWtb9W7B971dLuWAs1N:Math.NumberTheory.Powers.Squares前回は Out of memory が出たが、今回は違うエラーが出た。 エラーの種類は違うが、結局、「大きな素数」が大きすぎるのが問題である。
前回も書いたように、 arithmoi パッケージの素数列挙アルゴリズムが扱える範囲には限りがある。 この場合の「大きな素数」は平気で 10^{40} のような大きさになるが、 arithmoi パッケージの素数列挙アルゴリズムではそのような大きな素数を扱えない。
そこで、2通りの方針が考えられる:
- 確実な素数判定をやめて、確率的な素数判定を使う;選んだ数が素数じゃなかったせいでアルゴリズムが失敗した場合は、別の「素数っぽい数」を選んでアルゴリズムをやり直す。
- 「大きな素数」を必要としないアルゴリズムを使う。
前者をプログラムで実装する際は、「アルゴリズムが失敗」した場合にどうやって復帰するかという問題がある。 例外など、大域脱出の方法が用意されている言語ではそれを使えば良いだろう。
Haskell でそういうことをやる場合は、 Maybe や Either 等のモナドを使うことになる。 しかし、 Haskell 標準の割り算は (/) :: Fractional a => a -> a -> a で、モナドじゃない純粋な処理を前提にしている。 これまでに実装した関数も、大域脱出は考慮していない。 演算が失敗する可能性を考慮してモナドを使うように書き換えるのも大変そうである。
そこで、この連載では後者の方針で進むことにする。 具体的には、Hensel の補題を使い、比較的小さな素数 p に対する mod p での因数分解の結果を、 mod p^l (p の冪乗) へ「持ち上げる」。 これによって、大きな法 (p^l) での因数分解が得られる。
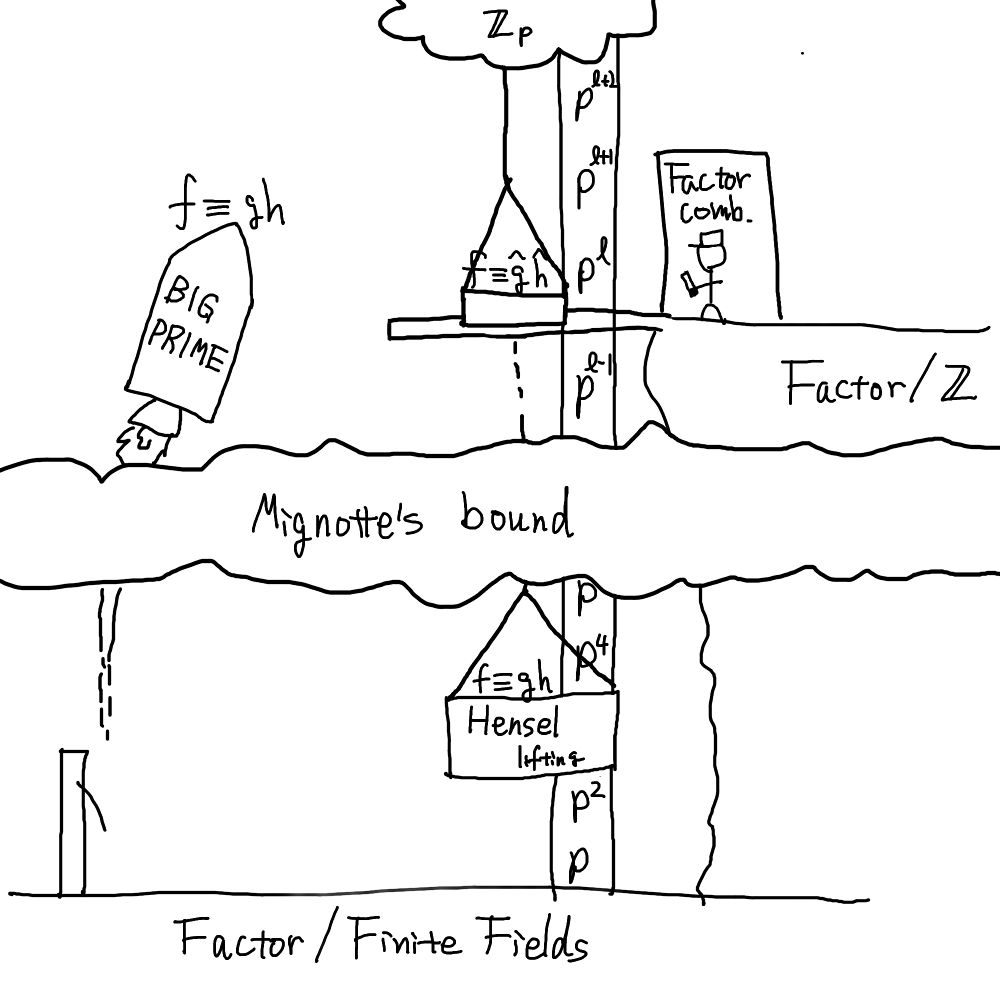
Hensel の補題
早速 Hensel の補題を紹介しよう。 名前は「補題」となっているが、立派な定理である。 定理は一般的な形で述べるが、気持ちとしては R=\mathbb{Z}, p は素数, f が因数分解したい多項式で、 g,h は事前に得られた mod p での因数分解結果と思って読んでくれて良い。
定理 (Hensel). R を可換環、 p\in R を 0 でない元とする。 f,g,h\in R[x] について、 \operatorname{lc}(f) は mod p での零因子ではなく、 h はモニックで、 f\equiv gh\mod p を満たし、 g と h について次のような s,t\in R[x] が存在するとする: \begin{gathered} sg+th\equiv 1\mod p, \\ \deg s<\deg h,\quad \deg t<\deg g \end{gathered} (f が定数でない場合は、このような s,t が存在するというのは g と h が mod p で互いに素であるということと同値である。)
このとき、正の整数 l それぞれに対し、以下を満たす g^*,h^*\in R[x] が存在する: f\equiv g^*h^*\mod{p^l} ただし、 g^*, h^* は g, h の mod p^l への「持ち上げ」、つまり \deg g=\deg g^*, \deg h=\deg h^* かつ g\equiv g^*, \quad h\equiv h^*\mod p で、 h^* はモニックである。
【1月29日 更新】定理の主張を微修正した。
見ればわかるように、g^*, h^* の係数には mod p^l の不定性がある。 しかし逆に、 g^*, h^* は mod p^l を除くと一意に定まる。
定理(Hensel 持ち上げの一意性). Hensel 持ち上げの g^*, h^* は mod p^l を除いて一意である。 つまり、 R, p を上記と同様に取り、 g^*,h^*,g^\dagger,h^\dagger\in R[x] が g^*\equiv g^\dagger, \quad h^*\equiv h^\dagger\mod p を満たし、ある s,t\in R[x] について sg^*+th^*\equiv 1\mod p が成り立つとする。 この時、正の整数 l について、 g^*h^*\equiv g^\dagger h^\dagger\mod p^l であれば g^*\equiv g^\dagger, \quad h^*\equiv h^\dagger\mod p^l である。
Hensel 持ち上げの一意性はここでは証明しない。
Hensel の補題は、次の Hensel step を m=p^k として繰り返し適用することにより証明できる。 つまり、 Hensel step を1回適用すれば l=2 の場合が示され、2回適用すれば l=4 の場合が示され(従って l=3 の場合も示される)、 k 回適用すれば l=2^k の場合が示され(従って l<2^k の場合も示される)、という具合である。
補題 (Hensel step). R を可換環、 m\in R を 0 でない元とする。 f,g,h,s,t\in R[x] であって \operatorname{lc}(f) は mod m での零因子ではなく、 h はモニックで、 \begin{gathered} f\equiv gh, \quad sg+th\equiv 1\mod m,\\ \deg s<\deg h, \quad \deg t<\deg g \end{gathered} を満たすとする。
このとき、以下を満たす g^*,h^*,s^*,t^*\in R[x] が存在する: \begin{aligned} f&\equiv g^*h^*\mod{m^2}, & s^*g^*+t^*h^*&\equiv 1\mod{m^2}, \\ g&\equiv g^*\mod m, & h&\equiv h^*\mod m, \\ \deg g&=\deg g^*, & \deg h&=\deg h^*, \\ \deg s^*&<\deg h^*, & \deg t^*&<\deg g^*. \end{aligned} ただし、 h^* はモニックである。
g^* と h^* の具体的な与え方を見ておこう。 まず e:=f-gh とおき、 se を h で割った商 q\in R[x] とあまり r\in R[x] se=qh+r, \quad \deg r<\deg h を考え、 \begin{aligned} g^*&:\equiv g+te+qg\mod m^2, \\ h^*&:\equiv h+r\mod m^2 \end{aligned} とおく。 ただし、e と se の計算は mod m^2 で行って良い。 それから、g+te+qg の R[x] での次数は \deg g よりも大きくなってしまうかもしれないが、次数の高い項の係数は mod m^2 で 0 になるので、mod m^2 では次数が \deg g^* と等しいと思える。
演習問題 このように定めた g^*, h^* が f\equiv g^*h^*\mod{m^2} を満たすことを確かめよ。 ヒント:e\equiv q\equiv r\equiv 0\mod{m} である。
s^* と t^* の与え方も見ておこう。 まず b:=sg^*+th^*-1 とおき、 sb を h^* で割った商 c\in R[x] とあまり d\in R[x] sb=ch^*+d, \quad \deg d<\deg h^* を考え、 \begin{aligned} s^*&:\equiv s-d\mod m^2, \\ t^*&:\equiv t-tb-cg^*\mod m^2 \end{aligned} とおく。 ただし、b と sb の計算は mod m^2 で行って良い。 それから、 t-tb-cg^* の R[x] での次数は \deg g^* よりも大きくなってしまうかもしれないが、次数の高い項の係数は mod m^2 で 0 になるので、mod m^2 では次数が \deg g^* 未満だと思える。
演習問題 このように定めた s^*, t^* が s^*g^*+t^*h^*\equiv 1\mod{m^2} を満たすことを確かめよ。 ヒント:b\equiv c\equiv d\equiv 0\mod{m} である。
注意深い方は気づいたかもしれないが、 g^*,h^*,s^*,t^* を構成する際に h や h^* による多項式除算を使っている。 通常は係数環が体でないと多項式除算はできないが、今回は h や h^* がモニックであるという仮定があるので、 R がただの可換環にも関わらず h や h^* による除算ができる。
注意 なお、次数についての制約を無視して単に \begin{gathered} f\equiv \hat{g}\hat{h},\quad \hat{s}\hat{g}+\hat{t}\hat{h}\equiv 1\mod m^2, \\ g\equiv\hat{g}, \quad h\equiv\hat{h}\mod m \end{gathered} を満たす \hat{g},\hat{h},\hat{s},\hat{t}\in R[x] が欲しいのであれば、 \begin{aligned} \hat{g}&:=g+te, \\ \hat{h}&:=h+se, \\ \hat{s}&:=s-sb, \\ \hat{t}&:=t-tb \end{aligned} とすれば良い。 (ちなみに、これらに対して多項式除算を適用して次数の条件を満たすようにすると g^*,h^*,s^*,t^* が得られる。)
例 R=\mathbb{Z}, p=5, f=3x^3+2x^2+x+3, g=3x^2+x+4, h=x+2 とおく。 g, h が f の mod 5 における因数分解となっていることは計算すればわかる: f=3x^3+2x^2+x+3\equiv \underbrace{(3x^2+x+4)}_{g}\underbrace{(x+2)}_{h}\mod 5 また、 s=4, t=-2x とおけば sg+th%=4(3x^2+x+4)-2x(x+2) =10x^2+16\equiv 1\mod 5 となるので、これらは Hensel の補題の前提を満たしている。
これらに対して、mod 25 への Hensel 持ち上げを計算しよう。 まず e を e:=f-gh=-5x^2-5x-5 とおく。 se を h で割った商 q と余り r は \begin{aligned} se&%=4(-5x^2-5x-5) =-20x^2-20x-20 \\ &=\underbrace{(-20x+20)}_{q}(x+2)\underbrace{-60}_{r} \end{aligned} より q=-20x+20, r=-60 である。 これらを使うと g^* は \begin{aligned} g^*\equiv g+te+qg%&=(3x^2+x+4)+(-2x)(-5x^2-5x-5)+(-20x+20)(3x^2+x+4) \\ &=-50x^3+53x^2-49x+84 \\ &\equiv 3x^2+x+9\mod 25 \end{aligned} で、 h^* は h^*\equiv h+r=x-58\equiv x-8\equiv x+17\mod 25 と計算できる。 つまり f は mod 25 で f=3x^3+2x^2+x+3\equiv \underbrace{(3x^2+x+9)}_{g^*}\underbrace{(x+17)}_{h^*}\mod 25 と因数分解できる。
s^* と t^* も計算しておこう。まず b を b:\equiv sg^*+th^*-1=10x^2+20x+35\equiv 10x^2-5x+10\mod 25 とおき、 sb を h^* で割った商 c と余り d を計算する: \begin{aligned} sb&\equiv 40x^2-20x+40%&\equiv 15x^2+5x+15 \mod 25 \\ &\equiv \underbrace{15x}_{c}(x+17)+\underbrace{15}_{d} \mod 25 \end{aligned} s^*, t^* は \begin{aligned} s^*&:=s-d=-11, \\ t^*&:\equiv t-tb-cg^*\equiv 8x\mod 25 \end{aligned} となる。 実際、 s^*g^*+t^*h^* を計算してみると s^*g^*+t^*h^*=-25x^2+125x-99\equiv 1\mod 25 となる。
例 さっきの例の結果 \underbrace{3x^3+2x^2+x+3}_{f}\equiv\underbrace{(3x^2+x+9)}_{g^*}\underbrace{(x+17)}_{h^*} \mod 25 にさらに Hensel step を適用し、因数分解を mod 5^4=625 へ持ち上げることもできる。
計算は大変なので結果だけ書くと、 g^*, h^* の mod 625 への持ち上げは \underbrace{3x^3+2x^2+x+3}_{f}\equiv\underbrace{(3x^2+301x+209)}_{g^{**}}\underbrace{(x+317)}_{h^{**}}\mod 625 となる(演習問題:この式が正しいことを確かめよ)。
まとめると \begin{aligned} 3x^3+2x^2+x+3&\equiv(3x^2+x+4)(x+2) \mod 5, \\ 3x^3+2x^2+x+3&\equiv(3x^2+x+9)(x+17) \mod 5^2, \\ 3x^3+2x^2+x+3&\equiv(3x^2+301x+209)(x+317) \mod 5^4 \end{aligned} である。
さらに繰り返し Hensel step を適用すれば mod 5^8, mod 5^{16} と、いくらでも大きい 5 の冪を法とした因数分解を得られる。
なお、 mod 5^4 での因数分解があれば、それより小さい冪、つまり mod 5^3 や mod 5^2, mod 5 での因数分解は直ちに得られる。 つまり、 3x^3+2x^2+x+3\equiv(3x^2+301x+209)(x+317) \mod 5^4 が与えられれば、適当に剰余を取ることによって(剰余を取らなくても良いが) \begin{aligned} 3x^3+2x^2+x+3&\equiv(3x^2+51x+84)(x+67) &&\mod 5^3, \\ 3x^3+2x^2+x+3&\equiv(3x^2+x+9)(x+17) &&\mod 5^2, \\ 3x^3+2x^2+x+3&\equiv(3x^2+x+4)(x+2) &&\mod 5 \end{aligned} を得ることができる。 つまり mod 5^4 での因数分解の方が mod 5 や mod 5^2 での因数分解よりも「情報量が多い/精度が高い」。 Hensel 持ち上げは、与えられた mod 5^i での因数分解の「情報量を増やす/精度を高める」ことにより mod 5^{2i} での因数分解を得る操作である。
演習問題 2x^2+4x+4\equiv (2x+3)(x+3) \mod 5 に Hensel の補題を適用し、mod 25 での f=2x^2+4x+4 の因数分解を計算せよ。 (ヒント:3(2x+3)-(x+3)\equiv 1\mod 5 である)
p 進数 (p-adic number) をご存知の方は、 Hensel の補題によって整数係数多項式の因数分解を p 進整数環を係数とする多項式環 \mathbb{Z}_p[x] での因数分解に持ち上げることができることが想像できるだろう。 しかし p 進数については今回は扱わない。
Hensel の補題を使った因数分解アルゴリズム
前回の「大きな素数を使う」アルゴリズムでは、 mod p での因数分解の結果を使ってすぐに「因数の組み合わせ」のステップに進んでいた。 今回の、 Hensel の補題を使うアルゴリズムでは、その間に「mod p での因数分解を mod p^l に持ち上げる」ステップが挟まる。
Hensel の補題は f=gh と2つの因数に分かれる場合を持ち上げるものだった。 因数分解への応用で必要なのは、 n 個の因数 f\equiv \operatorname{lc}(f)g_1g_2\cdots g_n\mod p (ただし各 g_i はモニック) を f\equiv \operatorname{lc}(f)g_1^*g_2^*\cdots g_n^*\mod{p^l} に持ち上げる作業である。
これにはヘンゼルの補題を繰り返し使えば良い。 具体的には、 g:=\operatorname{lc}(f)g_1\cdots g_k, \quad h:=g_{k+1}\cdots g_n とおいてヘンゼルの補題を適用し、 f\equiv g^*h^*\mod{p^l} を満たす g^*,h^*\in\mathbb{Z}[x] を得る。 次に g^*\equiv\operatorname{lc}(g^*)g_1g_2\cdots g_k, h^*\equiv g_{k+1}\cdots g_n\mod{p} に対して再帰的にアルゴリズムを適用する。
n=1 の場合は g_1^* は f に mod p^l での \operatorname{lc}(f) の逆数をかけたものになる。
ヘンゼルの補題を利用するには、 mod m で互いに素な g,h\in\mathbb{Z}[x] に対して sg+th\equiv 1\mod m となる s,t\in\mathbb{Z}[x] を見つける必要がある。 この操作は拡張ユークリッドの互除法 (EEA; extended Euclidean algorithm) で実装できる。
というわけで、今回の因数分解アルゴリズムは次のようになる:
入力は無平方原始多項式 f で、最高次の係数は正とする。
- 因数の係数の上限 B=\sqrt{n+1}\cdot 2^n\left\lVert f\right\rVert_\infty\cdot\operatorname{lc}(f) を計算する。
- 適切な素数 p を見つける。
- \operatorname{lc}(f) を割り切らない奇素数 p を選ぶ。
- f の mod p での像 \overline{f} が無平方かどうか確かめる。 つまり、 \gcd(\overline{f},\overline{f'}) が 1 となるかを見る。 無平方でなかった場合は、 i. に戻って別の素数を選ぶ。
- p^l\ge 2B+1 となるような自然数 l を計算する(つまり l:=\lceil\log_p(2B+1)\rceil)。
- 有限体上の因数分解アルゴリズムを使い、 \overline{f}\in\mathbb{F}_p[x] を因数分解する。 つまり、既約なモニック多項式 g_1,\ldots,g_r\in\mathbb{F}_p[x] によって \overline{f}=\overline{\operatorname{lc}(f)}g_1\cdots g_r と表す。
- Hensel の補題により、因数分解の結果を mod p^l に「持ち上げる」。 つまり、 f\equiv\operatorname{lc}(f)\hat{g}_1\cdots \hat{g}_r\mod{p^l}, \hat{g}_i\equiv g_i\mod{p} となるモニック多項式 \hat{g}_1,\ldots,\hat{g}_r\in\mathbb{Z}[x] を計算する。
- T:=\{1,\ldots,r\}, f^*:=f とおく。 k=1,2,\ldots について、以下を順番に実行する:
- 2k>\#T ならば f^* は既約であり、アルゴリズムを終了する。
- T の k 元部分集合 S (S\subset T,\#S=k) それぞれについて、以下を実行する:
- \hat{g}_1,\ldots,\hat{g}_r のうち、 S に対応するものの積を取る:g:=\operatorname{lc}(f^*)\prod_{i\in S} \hat{g}_i. 残り T\setminus S に対しても積を取る:h:=\operatorname{lc}(f^*)\prod_{i\in T\setminus S} \hat{g}_i.
- g, h の係数を mod p^l で (-p^l/2,p^l/2) の範囲に直す:それぞれ g^*\in\mathbb{Z}[x], h^*\in\mathbb{Z}[x] とおく。
- \left\lVert g^*\right\rVert_1\left\lVert h^*\right\rVert_1<B ならば、 g^*h^*=\operatorname{lc}(f^*)f^* である。 \operatorname{pp}(g^*) はアルゴリズムの結果となるべき f の因数である。 T:=T\setminus S, f^*:=\operatorname{pp}(h^*) とおき、 ii. に戻る。
「持ち上げ」のステップが挟まったこと以外は、前回と同様である。
実装
まず、拡張ユークリッドの互除法の実装を src/Numeric/AlgebraicReal/Class.hs に書き加える:
-- | 拡張ユークリッドの互除法
--
-- case exEuclid f g of (h, s, t) ->
-- h == gcdD f g (up to unit)
-- s * f + t * g == h
--
-- >>> exEuclid 32 63
-- (1,2,-1)
-- >>> exEuclid 28 63
-- (7,-2,1)
exEuclid :: (Eq a, EuclideanDomain a) => a -> a -> (a, a, a)
exEuclid f g = loop 1 0 0 1 f g
where loop u0 u1 v0 v1 f 0 = (f, u0, v0)
loop u0 u1 v0 v1 f g =
case divModD f g of
(q,r) -> loop u1 (u0 - q * u1) v1 (v0 - q * v1) g r「モニック多項式による除算」の実装を src/Numeric/AlgebraicReal/UniPoly.hs に書き加える:
-- | division by a monic polynomial
monicDivMod :: (Eq a, Num a) => UniPoly a -> UniPoly a -> (UniPoly a, UniPoly a)
monicDivMod f g
-- leadingCoefficient g must be 1
| leadingCoefficient g /= 1 = error "monicDivMod: g must be monic"
| otherwise = loop zeroP f
where
-- invariant: f == q * g + r
loop q r | degree r < degree g = (q, r)
| otherwise = loop (q + q') (r - q' * g)
where q' = UniPoly (V.drop (degree' g) (coeff r))今回実装する、 Hensel の補題関連のアルゴリズムは src/Numeric/AlgebraicReal/Factor/Hensel.hs に書く。
module Numeric.AlgebraicReal.Factor.Hensel where
import Prelude hiding (toInteger)
import Numeric.AlgebraicReal.Class
import Numeric.AlgebraicReal.UniPoly
import Numeric.AlgebraicReal.Factor.BigPrime (factorCoefficientBound,primeFieldFromInteger,coprimeModP,oneNorm,partitions)
import Numeric.AlgebraicReal.Factor.CantorZassenhaus (factorCZ)
import Data.FiniteField (PrimeField,char,toInteger)
import System.Random (RandomGen,getStdRandom)
import GHC.TypeLits (KnownNat,natVal)
import Data.Reflection (reifyNat)
import Data.Proxy (Proxy)
import Math.NumberTheory.Primes.Sieve (primes)
import Control.Monad (guard)import 部分は前回の BigPrime.hs と同様である。
まずは、2個の積に対する Hensel lifting を実装する。
-- Assumption:
-- f === g * h (mod p)
-- h is monic
-- Output (g',h'):
-- f === g' * h' (mod p^l)
-- h' is monic
henselLifting2 :: (KnownNat p) => Int -> UniPoly Integer -> UniPoly (PrimeField p) -> UniPoly (PrimeField p) -> (UniPoly Integer, UniPoly Integer)
henselLifting2 l f g h =
let (u,s,t) = exEuclid g h
-- s * g + t * h == u
g_ = mapCoeff toInteger g
h_ = mapCoeff toInteger h
s_ = mapCoeff toInteger (s `divide` u)
t_ = mapCoeff toInteger (t `divide` u)
in loop 1 p g_ h_ s_ t_
where
p = char (leadingCoefficient g)
g0 = mapCoeff toInteger g
h0 = mapCoeff toInteger h
loop i m g h s t | i >= l = (g, h)
| otherwise = loop (2 * i) (m^2) g' h' s' t'
where
-- Hensel step
-- Assumption:
-- f - g * h === 0 (mod m)
-- s * g + t * h === 1 (mod m)
-- h is monic
-- degree f = degree g + degree h
-- degree s < degree h
-- degree t < degree g
-- Output (g',h',s',t'):
-- f - g' * h' === 0 (mod m^2)
-- s' * g' + t' * h' === 1 (mod m)
-- h' is monic
-- g === g', h === h' (mod m)
-- s === s', t === t' (mod m)
-- degree g == degree g'
-- degree h == degree h'
-- degree s' < degree h'
-- degree t' < degree g'
e = mapCoeff (`mod` m^2) (f - g * h)
(q,r) = (s * e) `monicDivMod` h
g' = mapCoeff (`mod` m^2) (g + t * e + q * g)
h' = mapCoeff (`mod` m^2) (h + r)
b = mapCoeff (`mod` m^2) (s * g' + t * h' - 1)
(c,d) = (s * b) `monicDivMod` h'
s' = mapCoeff (`mod` m^2) (s - d)
t' = mapCoeff (`mod` m^2) (t - t * b - c * g')コメントを長々と書いた。
有限体の演算は PrimeField p 型を使ったが、 mod p^l での演算には専用の型を使わないことにする。 これは、 #1 で実装した多項式演算が、係数が整域であることを仮定しているためである。
拡張ユークリッドの互除法を使って mod p^l での逆数を計算する関数を用意する:
inverseMod :: Integer -> Integer -> Integer
inverseMod x m = case exEuclid x m of
-- s == t * x + _ * m
(s,t,_) | s == 1 || s == -1 -> s * t
| otherwise -> error (show x ++ " has no inverse modulo " ++ show m)これを使って、 Hensel の補題を n 個の多項式の積へ一般化したものを実装する:
-- Assumption:
-- f === leadingCoefficient f * product gs (mod p)
-- gs are monic
-- Output:
-- let gs' = henselLift l f gs
-- f === leadingCoefficient f * product gs' (mod p^l)
-- gs' are monic
henselLifting :: (KnownNat p) => Int -> UniPoly Integer -> [UniPoly (PrimeField p)] -> [UniPoly Integer]
henselLifting l f [] = [] -- f must be 1
henselLifting l f [g] = [mapCoeff (\a -> inv_lc_f * a `mod` (p^l)) f] -- f == g
where inv_lc_f = inverseMod (leadingCoefficient f) (p^l)
p = char (leadingCoefficient g)
henselLifting l f gs =
let (gs1,gs2) = splitAt (length gs `div` 2) gs
g = fromInteger (leadingCoefficient f) * product gs1
h = product gs2
(g',h') = henselLifting2 l f g h
in henselLifting l g' gs1 ++ henselLifting l h' gs2あとは前回同様である。 「整数係数の無平方な原始多項式(最高次の係数は正)」を因数分解する関数の名前は factorHensel とする:
-- Input: nonzero, primitive, squarefree
factorHensel :: (RandomGen g) => UniPoly Integer -> g -> ([UniPoly Integer], g)
factorHensel f =
let lc_f = leadingCoefficient f
bound = factorCoefficientBound f * lc_f
p:_ = filter (\p -> lc_f `mod` p /= 0 && reifyNat p coprimeModP f (diffP f)) $ tail primes
in reifyNat p factorWithPrime bound f
factorHenselIO :: UniPoly Integer -> IO [UniPoly Integer]
factorHenselIO f = getStdRandom (factorHensel f)素数の選び方に関して、素朴に「3 以上の素数で条件を満たす最小のもの」としている。
素数を選んだ後の処理は前回同様、 factorWithPrime 関数に分けた:
-- p must be prime
factorWithPrime :: (KnownNat p, RandomGen g) => Proxy p -> Integer -> UniPoly Integer -> g -> ([UniPoly Integer], g)
factorWithPrime proxy bound f gen =
let p = natVal proxy
f' = toMonic $ mapCoeff (primeFieldFromInteger proxy) f -- :: UniPoly (PrimeField p)
(modularFactorsP, gen') = factorCZ f' gen
-- Choose l and m so that m = p^l > 2 * bound + 1
(l,m) | p^l' > 2 * bound + 1 = (l',p^l')
| otherwise = head $ filter (\(i,m) -> m > 2 * bound + 1) $ iterate (\(i,m) -> (i + 1, m * p)) (l',p^l')
where l' = ceiling (log (fromInteger (2 * bound + 1) :: Double) / log (fromInteger p :: Double)) :: Int
modularFactors = henselLifting l f modularFactorsP
-- f === leadingCoefficient f * product modularFactors (mod p^l)
in (factorCombinationsModulo m bound 1 f modularFactors, gen')p^l が十分大きくなるような l を計算するのに、 Double 型の不正確な演算を使っている。 もっとうまい書き方があるかもしれないが、今はこれでいく。
因数の組み合わせを試すステップも、だいたい前回と同様である。 ただし、前回は法となる素数を型レベルで渡していたが、今回は最初の引数として渡している。
-- m >= 2 * bound + 1
-- f === leadingCoefficient f * product modularFactors (mod m)
factorCombinationsModulo :: Integer -> Integer -> Int -> UniPoly Integer -> [UniPoly Integer] -> [UniPoly Integer]
factorCombinationsModulo m bound k f modularFactors = loop k f modularFactors
where loop k f [] = [] -- f must be 1
loop k f modularFactors
| 2 * k > length modularFactors = [f] -- f is already irreducible
| otherwise = case tryFactorCombinations of
[] -> loop (k+1) f modularFactors
(g,h,rest):_ -> g : loop k h rest
where tryFactorCombinations = do
(s,rest) <- partitions k modularFactors
-- length s == k, s ++ rest == modularFactors (as a set)
let lc_f = fromInteger (leadingCoefficient f)
g = mapCoeff toInteger_ (lc_f * product s)
h = mapCoeff toInteger_ (lc_f * product rest)
guard (oneNorm g * oneNorm h <= bound)
return (primitivePart g, primitivePart h, rest)
toInteger_ :: Integer -> Integer
toInteger_ n = case n `mod` m of
k | 2 * k > m -> k - m
| otherwise -> kコードを書き終わったら、 algebraic-real.cabal に今回のモジュール名 Numeric.AlgebraicReal.Factor.Hensel を追加する:
exposed-modules: Numeric.AlgebraicReal.UniPoly
...
, Numeric.AlgebraicReal.Factor.Berlekamp
, Numeric.AlgebraicReal.Factor.BigPrime
, Numeric.AlgebraicReal.Factor.Hensel試す
例によって stack repl を使って試してみよう。
$ stack repl
...
......> :set prompt "> "
> :m + System.Random
> setStdGen (mkStdGen 346525153451)
> let x = ind
> :set +s前回の「大きな素数」を使うアルゴリズムでは x^{100}-1 の因数分解が Out of memory のためできなかった。 今回のアルゴリズムではどうだろうか。
> factorHenselIO $ x^100 - 1
[UniPoly [1,1],UniPoly [-1,1],UniPoly [1,0,1],UniPoly [1,1,1,1,1],UniPoly [1,-1,1,-1,1],UniPoly [1,0,0,0,0,-1,0,0,0,0,1,0,0,0,0,-1,0,0,0,0,1],UniPoly [1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1],UniPoly [1,0,-1,0,1,0,-1,0,1],UniPoly [1,0,0,0,0,0,0,0,0,0,-1,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,-1,0,0,0,0,0,0,0,0,0,1]]
(12.62 secs, 5,549,835,752 bytes)12秒と、決して一瞬と呼べるほどではないが、何かしらの因数分解結果が得られた。 検算しておこう。
> product it
UniPoly [-1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1]
(0.02 secs, 4,363,768 bytes)
> it == x^100 - 1
True
(0.02 secs, 4,094,392 bytes)代数的実数のアルゴリズムに使う
src/Numeric/AlgebraicReal/AlgReal.hs を編集し、今回実装したアルゴリズムを使うようにする。
まず、ファイル先頭の import 部の
import Numeric.AlgebraicReal.Factor.BigPrimeを消して
import Numeric.AlgebraicReal.Factor.Henselを追加する。
あとは、 factorIntIO を呼んでいる2箇所を factorHenselIO に置き換える。
さっきと同じように REPL を起動しよう。 冒頭で紹介した、「*** Exception: integerSquareRoot: negative argument が出て失敗する例」を試してみよう:
> let [a0,a1,a2,a3] = realRoots (x^8-4*x^7+2*x^6+4*x^5-5*x^4+12*x^3-18*x^2+9)
(0.04 secs, 365,560 bytes)
> (a0 - 1 - sqrtQ 2) * a0 - sqrtQ 3
AlgReal (UniPoly [36864,0,-9216,3072,-320,-128,80,-16,1]) (-1) (4385570535 % 1073741824) (153992357 % 33554432)
(601.56 secs, 234,329,095,992 bytes)REPL では10分以上かかった(コンパイルして最適化すれば4分程度で完了する)ものの、一応結果が出た。
【1月29日 追記】 この計算において、時間の大半は因数分解ではなく終結式の計算に費やされている。 よって、高速化するなら因数分解ではなく終結式の方が優先順位が高い。
【7月12日 更新】 Hensel持ち上げの一意性についての注釈と、Hensel持ち上げの例を追加した。